Ana səhifə :: Riyaziyyat :: Həndəsə :: Dördbucaqlı
Yaranma tarixi:
Paraleloqram
dördbucaqlı paraleloqram əlamətlər xassə
Qarşı tərəfləri paralel olan dördbucaqlıya paraleloqram deyilir.
Paraleloqramın xassələri
Teorem 1: Paraleloqramın qarşı tərəfləri bərabərdir, qarşı bucaqları bərabərdir, bir tərəfə söykənən bucaqlarının cəmi $180°$-yə bərabərdir.

Şəkil 1
İsbatı: $ABCD$ paraleloqramı verilib (şəkil 1). İsbat etməliyik ki, $AD=BC$, $AB=DC$, $\angle DAB=\angle BCD$, $\angle ADC = \angle CBA$, $\angle BAD + \angle ADC = 180°$, $\angle ADC + \angle DCB = 180°$, $\angle DCB + \angle CBA = 180°$, $\angle CBA + \angle BAD = 180°$.
Əvvəla $\angle BAD$ və $\angle ADC $ iki paralel xəttin üçüncü ilə kəsişməsindən alınan birtərəfli bucaqlar olduğundan bunların cəmi $180°$-dir. Eyni sözü digər $\angle ADC$ və $\angle DCB$, $\angle DCB$ və $ \angle CBA$, $\angle CBA$ və $\angle BAD$ birtərəfli bucaqları barədə də demək olar.
İndi paraleloqramın $AC$ diaqonalını çəkək. Bu diaqonal paraleloqramı iki üçbucağa bölür. Alınan $\triangle ACD$ və $\triangle ACB$-də $AC$ tərəfləri ortaqdır. $\angle CAB = \angle ACD$ və $\angle DAC = \angle BCA$, çünki bunlar daxili çarpaz bucaqlardır. Onda üçbucaqların bərabərliyinin ikinci əlamətinə görə $\triangle ACB = \triangle ACD$. Bu bərabərlikdən isə uyğun bucaqların və uyğun tərəflərin bərabərliyi alınır. Yəni, $AB = DC$, $AD=BC$, $\angle ADC=\angle CBA$.
Eynilə $BD$ diaqonalı çəksək, $\triangle ABD=\triangle CBD$ alırıq ki, bunların da bərabərliyindən $\angle DAB=\angle BCD$ alınır.
Teoremin bütün hökmləri isbat olundu.
Teorem 2: Paraleloqramın diaqonalları kəsişmə nöqtəsində yarı bölünür.

Şəkil 2
İsbatı: Şəkil 2-dəki paraleloqrama nəzər salaq. Diaqonallar bu paraleloqramı 4 üçbucağa bölür. $\triangle AOB$ və $\triangle COD$-yə nəzər salaq. $\angle CDO=\angle ABO$ və $\angle DCO = \angle BAO$, çünki bunlar iki parallel xəttin üçüncü ilə kəsişməsindən alınan çarpaz bucaqlardır. Teorem 1-ə görə isə $AB=DC$. Onda üçbucaqların bərabərliyinin ikinci əlamətimə görə $\triangle AOB = \triangle COD$.
Buradan alınır ki, $AO=OC$ və $BO=OD$. Teorem isbat olundu.
Teorem 3: Paraleloqramın tərəflərinin kvadratları cəmi onun diaqonallarının kvadratları cəminə bərabərdir.
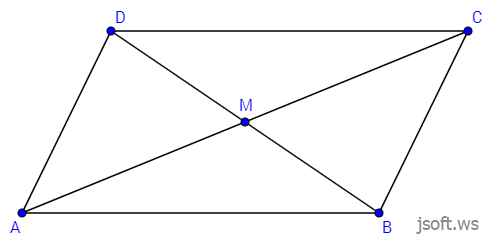
Şəkil 3
İsbatı: Bu teoremi şəkil 3-dəki $ABCD$ paraleloqramı üzərində isbat edək. Kosinuslar teoreminə görə $\triangle ABD$ -dən
$(1)$
Eynilə $\triangle ACD$-dən
$(2)$
$AC^2 = AD^2+CD^2-2 AD \cdot CD \cdot cos D$
$ABCD$ paraleloqram olduğu üçün $AB=CD$ və $\angle A$ ilə $\angle D$ iki paralel düz xəttin üçüncü ilə kəsişməsindən alınan daxili birtərəfli bucaqlardır. Deməli, $\angle D = 180°-\angle A$. Onda
$cos D = cos (180°- A) = cos 180° cos A+sin 180°sin A = -cos A$
$CD$ tərəfi və $cos D$ uçun bu əvəzləməni (2) bərabərliyində yerinə yazsaq
$(3)$
$AC^2 = AB^2+AD^2+2AB \cdot AD \cdot cos A$
alarıq. (1) və (3) bərabərliyini toplasaq aşağıdakı bərabərliyi alarıq ki, bu da teoremin isbatı deməkdir.
$AC^2 + BD^2 = 2(AB^2+AD^2)$
Paraleloqramın əlamətləri
Teorem (I əlamət): Əgər dördcucaqlının iki tərəfi paralel və bərabərdirsə, bu dördbucaqlı paraleloqramdır.

Şəkil 4
İsbatı: Tutaq ki, şəkil 4-dəki $ABCD$ dördbucaqlısında $AB \parallel CD$ və $AB=CD$. Bu dördbucaqlının $DB$ diaqonalı onu iki üçbucağa bölür, $\triangle ADB$ və $\triangle CBD$. Şərtə görə $AB=CD$. $BD$ tərəfi isə ortaqdır. $\angle ABD$ və $\angle CDB$ paralel $AB$ və $CD$ xətlərinin üçüncü xətlə kəsişməsindən alınan çarpaz bucaqlar olduğundan bərabərdir. Deməli üçbucaqların bərabərliyinin birinci əlamətinə görə $\triangle ADB = \triangle CBD$.
Deməli bu üçbucaqların uyğun bucaqları da bərabərdir. Yəni $\angle ADB = \angle CBD$. Bunlar isə daxili çarpaz bucaqlardır. Onda düz xətlərin paralelliyinin ikinci əlamətinə görə $AD \parallel BC$. Yəni $ABCD$ dördbucaqlısı paraleloqramdır.
Teorem (II əlamət): Əgər dördbucaqlının qarşı tərəfləri bərabərdirsə, bu dördbucaqlı paraleloqramdır.

Şəkil 5
İsbatı: Şəkil 5-də şərtə görə $AD=BC$, $AB=DC$. $BD$ tərəfi isə üçbucaqların ortaq tərəfidir. Deməli, $\triangle ADB= \triangle CBD$. Bu isə $ABD$ və $CDB$ çarpaz bucaqlarının bərabərliyi deməkdir. Yəni $AB \parallel CD$. Teoremin şərtinə görə isə $AB=DC$. Onda paraleloqramın birinci əlamətinə görə bu dördbucaqlı paraleloqramdır.
Teorem (III əlamət): Əgər dördbucaqlının diaqonalları kəsişib kəsişmə nöqtəsində yarı bölünürsə bu dördbucaqlı paraleloqramdır.
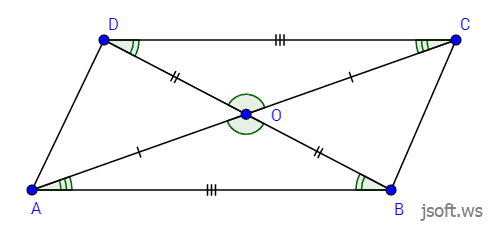
Şəkil 6
İsbatı: Şəkil 6-ya baxsaq görərik ki, üçbucaqların bərabərliyinin birinci əlamətinə görə $\triangle AOB = \triangle COD$, çünki $AO=OC$, $BO=OD$, $\angle AOB = \angle COD$ (qarşılıqlı bucaqlardır). Üçbucaqların bərabərliyindən alınır ki, $\angle ABO = \angle CDO$. Bunlar isə çarpaz bucaqlardır. Deməli, $AB \parallel CD$.
Həmçinin bu tərəflər bərabər üçbucaqların uyğun tərəfləri olduğundan bərabərdirlər ($AB=CD$). Onda paraleloqramın birinci əlamətinin şərtləri ödəndiyi üçün bu dördbucaqlı paraleloqramdır.
Digər məqalələr

Dördbucaqlı
Dörd təpəsi və bu təpələri ardıcıl birləşdirən dörd tərəfi olan fiqura dördbucaqlı deyilir. Heç bir üç təpə bir düz xətt üzərində yerləşə bilməz və onları birləşdirən parçalar kəsişməməlidir.

Ptolemey teoremi
Çevrə daxilinə çəkilmiş dördbucaqlının diaqonallarının hasili qarşı tərəflərin hasilləri cəminə bərabərdir.

Tebo teoremləri
Paraleloqramın tərəfləri üzərində qurulmuş kvadratların mərkəzləri özü, kvadratın təpə nöqtələridir. Əgər kvadratın iki qonşu tərəfində bərabərtərəfli üçbucaq qursaq bu üçbucaqların kvadrata aid olmayan təpələri ilə kvadratın bu üçbucaqlara aid olmayan təpəsini birləşdirərkən bərabərtərəfli üçbucaq alarıq.

Trapesiya
Yalnız iki qarşı tərəfi paralel olan qabarıq dördbucaqlıya trapesiya deyilir. Bu paralel tərəflərə trapesiyanın oturacaqları, paralel olmayan tərəflərə isə yan tərəfləri deyilir. Trapesiyanın qarşı təpələrini birləşdirən düz xətt parçasına onun diaqonalı deyilir.

Dördbucaqlı üçün Van-Obel teoremi
İxtiyarı dördbucaqlının tərəflərində xarici kvadratlar qursaq, qarşılıqlı kvadratların orta nöqtələrini birləşdirən düz xətt parçaları bərabər və perpendikulyar olacaq.

Dördbucaqlının sahəsi
Qabarıq dördbucaqlının sahəsi onun diaqonalları ilə bu diaqonalların kəsişmə nöqtəsində əmələ gələn bucağın sinusu hasilinin yarısına bərabərdir. Əgər bu dördbucaqlının xaricinə çevrə çəkmək mümkündürsə onun sahəsini Braxmaqupta düsturu vasitəsi ilə də tapmaq olar.

Varinyon teoremi
İstənilən dördbucaqlının tərəflərinin orta nöqtəsini birləşdirsək paraleloqram alarıq. Bu teoremdə dördbucaqlının qabarıq olması şərt deyil və bütün dördbucaqlılar üçün doğrudur.
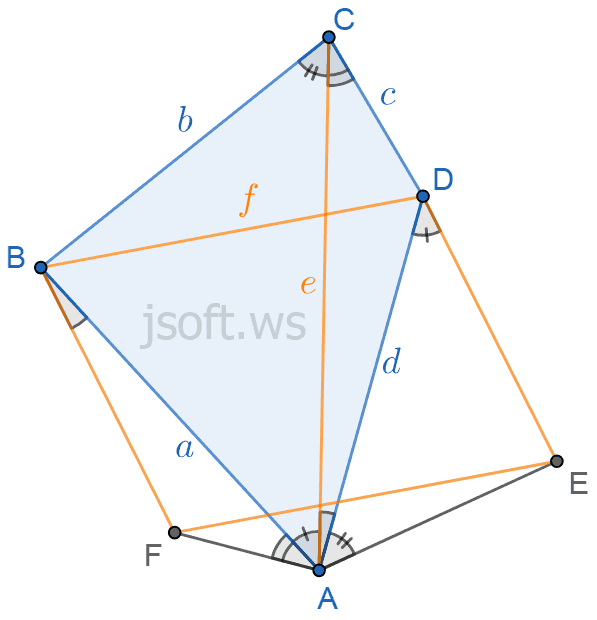
Bretşnayder teoremi
Bretşnayder teoreminə bəzi mənbələrdə Bretşnayder münasibəti də deyilir. Əslində bu teoremi dördbucaqlı üçün kosinuslar teoremi adlandırmaq olar. Həmin teoremin isbatını bu məqalədə oxuya bilərsiniz.
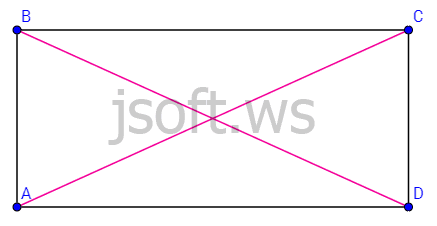
Düzbucaqlı, romb, kvadrat
Bütün bucaqları düz bucaq olan paraleloqrama düzbucaqlı deyilir. Bütün tərəfləri bərabər olan paraleloqrama romb deyilir. Bütün tərəfləri bərabər olan düzbucaqlı kvadrat adlanır.

Paralel xətlər
Müstəvi üzərində yerləşən xətlər ya bir nöqtədə kəsişir, ya da ümumiyyətlə kəsişmir. Müstəvidə kəsişməyən xətlərə paralel xətlər deyilir.

Çoxbucaqlı
Qonşu tərəfləri bir düz xətt üzərində olmayan və qonşu olmayan tərəfləri ümumi nöqtəyə malik olmayam qapalı fiqura çoxbucaqlı deyilir. Əgər çoxbucaqlı istənilən tərəfdən keçən xəttə nəzərən bütünlüklə bir yarımmüstəvidə yerləşirsə, ona qabarıq çoxbucaqlı deyilir.

Perpendikulyar və mail
Əgər düz xətt xaricindəki nöqtədən bu düz xəttə doğru çəkilən xəttin onunla əmələ gətirdiyi bucaq düz bucaq olarsa, bu xətlər perpendikulyar xətlər adlanır. Əgər düz xətt xaricindəki nöqtədən bu düz xəttə doğru çəkilən xəttin onunla əmələ gətirdiyi bucaq düz bucaqdan fərqlidirsə, bu xəttə mail deyilir.

Qurma məsələləri
Qurma məsələsi dedikdə həmişə fiqurun yalnız xətkeş və pərgarın köməyilə qurulması nəzərdə tutulur. Xətkeş vasitəsilə yalnız düz xətt çəkmək mümkündür. Xətkeş vasitəsilə ölçmə əməliyyatı aparmaq olmaq. Pərgar vasitəsilə çevrə çəkmək, və ya xətt üzərində verilmiş ölçülü parça ayırmaq mümkündür.
© Müəllif hüquqları qorunur
Bu saytdakı bütün məqalələr Cəfər N.Əliyev tərəfindən yazılıb. Onlar hər hansı üçüncu şəxs tərəfindən digər resurslarda çap edilərsə mənbə və müəllifin adı göstərilməlidir. Sayt özü həmin şərtlərə əməl edir.
