Yaranma tarixi: 20 İyul, 2017

Çoxbucaqlı

Təsəvvür edin ki, $AB$, $BC$, $CD$, ... ,$EF$, $FA$ birləşmiş parçaları var. $AB$ və $BC$, $BC$ və $CD$, nəhayət $FA$ və $AB$ qonşu parçalardır. Bu qonşu parçalar bir düz xətt üzərində olmamalıdır. Qonşu parçaları bir düz xətt üzərində olmayan və qonşu olmayan parçaları ümumi nöqtəyə malik olmayam qapalı fiqura çoxbucaqlı deyilir. $A$, $B$, $C$, .., $F$ çoxbucaqlının təpə nöqtələri,  $AB$, $BC$, .., $FA$ isə onun tərəfləridir. Bütün tərəflərin uzunluqları cəminə çoxbucaqlının perimetri deyilir.

$n$ sayda təpəsi olan çoxbucaqlıya $n$-bucaqlı deyilir. Şəkildə $A_1A_2A_3A_4A_5$ beşbucaqlısı verilib. Onun  yanındakı $C_1C_2C_3C_4C_5$ isə çoxbucaqlı deyil, çünki $C_1C_5$ və $C_2C_3$ qonşu olmayan parçalar olsalar da ümumi nöqtəyə malikdirlər.

Çoxbucaqlının bir tərəfinə  aid olan təpələrə qonşu təpələr deyilir. Qonşu olmayan təpələri birləşdirən parçalar diaqonal adlanır.

İstənilən çoxbucaqlı müstəvini iki hissəyə ayırır ki, bunlara daxili və xarici oblastlar deyilir.

Qabarıq çoxbucaqlı

Əgər çoxbucaqlı istənilən tərəfdən keçən xəttə nəzərən bütünlüklə bir yarımmüstəvidə yerləşirsə, ona qabarıq çoxbucaqlı deyilir. Yuxarıdakı şəkildə  $A_1A_2A_3A_4A_5$ çoxbucaqlısı qabarıq deyil. Aşağıdakı şəkildə isə $B_1B_2B_3…B_{n-1}B_n$ qabarıqdır. $\angle B_nB_1B_2$, $\angle B_1B_2B_3$, $\angle B_2B_3B_4$,...,$\angle B_{n-1}B_nB_1$ bu $n$-bucaqlının bucaqlarıdır.

Bu $n$-bucaqlıda $B_1$ təpəsindən çıxan bütün diaqonalları çəksək, nəticədə $n-2$ sayda diaqonal, və həmin sayda üçbucaq alarıq. Bu üçbucaqların daxili bucaqlarının cəmi $n$-bucaqlının daxili bucaqlarının cəmini verəcək. Bunların da hər biri $180°$-yə bərabər olduğu üçün çoxbucaqlının daxili bucaqlarının cəmi $(n-2)\cdot 180°$ olacaq. Xüsusi hal kimi qabarıq dördbucaqlıya baxsaq, $(4-2) \cdot 180° = 2 \cdot 180° = 360°$. Qabarıq dördbucaqlının daxili bucaqlarının cəmi $360°$-yə bərabərdir.

Bu düsturdan qabarıq çoxbucaqlının xarici bucaqlarının cəmi üçün düstur ala bilərik. Hər təpədəki daxili və xarici bucaqlar birlikdə açıq bucaq əmələ gətirdiyi üçün qonşu bucaqların cəmi isə $180°$ olduğu üçün xarici bucaqların cəmini belə hesablaya bilərik. Aşağıdakı düsturda $B_1’$, $B_2’$, $B_3’$, ..., $B_n’$ uyğun olaraq $B_1$, $B_2$, $B_3$, ..., $B_n$ bucaqlarının xarici bucaqlarıdır.

$B_1’ + B_2’ + ... +B_n’ = (180-B_1)+(180-B_2)+ ... + (180-B_n) = n \cdot 180 – (B_1+B_2 + ... +B_n) $

Qabarıq $n$-bucaqlının daxili bucaqların cəmini isə artıq bilirik. Onda,

$B_1’ + B_2’ + ... +B_n’ = n\cdot 180 – (n-2)\cdot 180 = (n-n+2) \cdot 180 = 2 \cdot 180 = 360°$

Deməli, bucaqlarının sayından asılı olmayaraq qabarıq çoxbucaqlının xarici bucaqlarının cəmi həmişə $360°$-yə bərabərdir.

Düzgün çoxbucaqlı

Bütün tərəfləri və bütün bucaqları bərabər olan çoxbucaqlıya düzgün çoxbucaqlı deyilir. Bərabərtərəfli üçbucaq və kvadrat düzgün çoxbucaqlıya misaldır.

Yuxarıda gördük ki, qabarlq çoxbucaqlının daxili bucaqlarının cəmi $(n-2)\cdot 180°$-dir. Düzgün çoxbucaqlının bütün bucaqları bərabər olduğu üçün onun hər bir təpə bucağı bu çəmin $n$-dən bir hissəsinə bərabər olacaq.

$\alpha_n = \dfrac{n-2}{n}\cdot 180°$

Digər məqalələr

Paralel xətlər

Müstəvi üzərində yerləşən xətlər ya bir nöqtədə kəsişir, ya da ümumiyyətlə kəsişmir. Müstəvidə kəsişməyən xətlərə paralel xətlər deyilir.

Sadə fiqurların sahəsi

Üçbucaq, düzbucaqlı, trapesiya, paraleloqram və rombun sahə düsturları yəqin ki, məktəb kursundan yadınızdadır. Bəs bu sahə düsturlarının çıxarılışı necə? O da yadınızadadırmı? Əgər unutmusunuzsa oxuyub hamısını bir dəfəyə yada salın.

Tək və cüt funksiyalar

Cüt funksiya elə funksiyadır ki, eyni arqumentin mənfi və müsbət qiymətlərində funksiyanın qiyməti bərabər olur. Tək funksiya elə funksiyadır ki, eyni arqumentin mənfi və müsbət qiymətlərində funksiyanın qiyməti də əksinə dəyişir.

Üçbucaqların bərabərlik əlamətləri

İki tərəf və arasındakı buçağı bərabər olan üçbucaqlar bərabərdir. Bir tərəf və ona söykənən bucaqları bərabər olan üçbucaqlar bərabərdir.

Perpendikulyar və mail

Əgər düz xətt xaricindəki nöqtədən bu düz xəttə doğru çəkilən xəttin onunla əmələ gətirdiyi bucaq düz bucaq olarsa, bu xətlər perpendikulyar xətlər adlanır. Əgər düz xətt xaricindəki nöqtədən bu düz xəttə doğru çəkilən xəttin onunla əmələ gətirdiyi bucaq düz bucaqdan fərqlidirsə, bu xəttə mail deyilir.

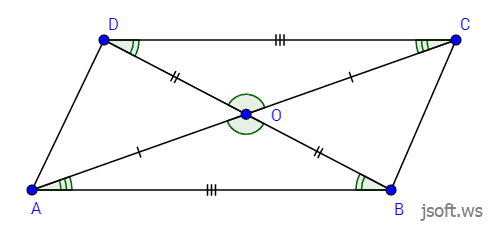
Paraleloqram

Paraleloqramın qarşı tərəfləri bərabərdir, qarşı bucaqları bərabərdir, bir tərəfə söykənən bucaqlarının cəmi 180°-yə bərabərdir. Paraleloqramın diaqonalları kəsişmə nöqtəsində yarı bölünür.

Qurma məsələləri

Qurma məsələsi dedikdə həmişə fiqurun yalnız xətkeş və pərgarın köməyilə qurulması nəzərdə tutulur. Xətkeş vasitəsilə yalnız düz xətt çəkmək mümkündür. Xətkeş vasitəsilə ölçmə əməliyyatı aparmaq olmaq. Pərgar vasitəsilə çevrə çəkmək, və ya xətt üzərində verilmiş ölçülü parça ayırmaq mümkündür.

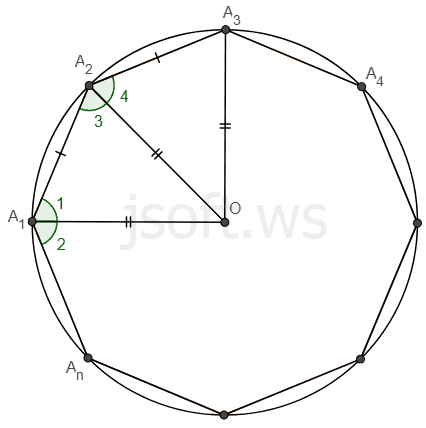
Düzgün çoxbucaqlının xaricinə və daxilinə çəkilmiş çevrələr

Əgər çoxbucaqlının bütün təpələri çevrə üzərindədirsə, bu çevrəyə çoxbucaqlının xaricinə çəkilmiş çevrə deyilir. Əgər çoxbucaqlının bütün tərəfləri çevrəyə toxunursa, bu çevrəyə çoxbucaqlı daxilinə çəkilmiş çevrə deyilir. İstənilən düzgün çoxbucaqlının xaricinə və daxilinə həmişə çevrə çəkmək olar.