Yaranma tarixi: 19 Mart, 2018

Dördbucaqlının sahəsi

Əvvəlcə onu deyək ki, istənilən dördbucaqlının sahəsini tapmaq üçün bu dördbucaqlını iki qarşı təpəsini birləşdirərək iki üçbucağa bölmək olar. Sonra isə bu üçbucaqların sahələrini tapıb toplamaq lazım olacaq. Hətta dördbucaqlı qabarıq olmasa belə onu şəkildəki kimi iki üçbucağa ayırmaq olar.

Qabarıq dördbucaqlının sahəsi

Qabarıq dördbucaqlının sahəsini onun diaqonalları vasitəsilə belə ifadə etmək olar.

$S=\dfrac{1}{2} d_1 d_2 sin \varphi$

Burada $d_1$ və $d_2$ diaqonallar, $\varphi$ isə bu diaqonalların kəsişməsindən alınan dörd bucaqdan biridir.

Bu düsturun çıxarılışına baxaq. Dördbucaqlını şəkildəki kimi 4 ədəd üçbucağa bölək və bu üçbucaqların sahələrini tapaq. Aydındır ki, həmin sahələrin cəmi bizə dördbucaqlının sahəsini verəcək.

$S = S_{\triangle AOB}+ S_{\triangle BOC}+ S_{\triangle COD}+ S_{\triangle DOA}$

Üçbucaqların sahələrini iki tərəf və arasındakı bucağın sinusu vasitəsi ilə tapaq.

$S_{\triangle AOB}=\dfrac{1}{2} AO \cdot BO \cdot sin \varphi \\[15pt]
S_{\triangle BOC}=\dfrac{1}{2} BO \cdot CO \cdot sin (\pi - \varphi) =\dfrac{1}{2} BO \cdot CO \cdot sin \varphi \\[15pt]
S_{\triangle COD}=\dfrac{1}{2} CO \cdot DO \cdot sin  \varphi \\[15pt]
S_{\triangle DOA} = \dfrac{1}{2} DO \cdot AO \cdot sin (\pi - \varphi) = \dfrac{1}{2} DO \cdot AO \cdot sin \varphi$

Bu düsturları toplayaq

$S=\dfrac{1}{2} (AO \cdot BO + BO \cdot CO + CO \cdot DO+ DO \cdot AO) sin \varphi =\\[15pt]
=\dfrac{1}{2} \left( (AO+CO) BO + (AO+CO)DO \right) sin \varphi =\\[15pt]
=\dfrac{1}{2}  (AO+CO) (BO +DO) sin \varphi$

Şəkildən görünür ki,

$AO+CO=AC=d_1, \ BO+DO=BD=d_2$

Bu əvəzləmələri aparsaq teorem isbat olunar.

Çevrə daxilinə çəkilmiş dördbucaqlının sahəsi

Əgər dördbucaqlı çevrə daxilinə çəkilibsə onun sahəsini tərəflər vasitəsilə belə tapmaq olar.

$S=\sqrt{(p-a)(p-b)(p-c)(p-d)}, \ \ p=\dfrac{a+b+c+d}{2}$

$a$, $b$, $c$, $d$ tərəflər, $p$ isə perimetrin yarısıdır. Buna Brahmaqupta teoremi deyilir və çıxarılışını eyni adlı məqalədən oxuya bilərsiniz.

Digər məqalələr

Dördbucaqlı

Dörd təpəsi və bu təpələri ardıcıl birləşdirən dörd tərəfi olan fiqura dördbucaqlı deyilir. Heç bir üç təpə bir düz xətt üzərində yerləşə bilməz və onları birləşdirən parçalar kəsişməməlidir.

Ptolemey teoremi

Çevrə daxilinə çəkilmiş dördbucaqlının diaqonallarının hasili qarşı tərəflərin hasilləri cəminə bərabərdir.

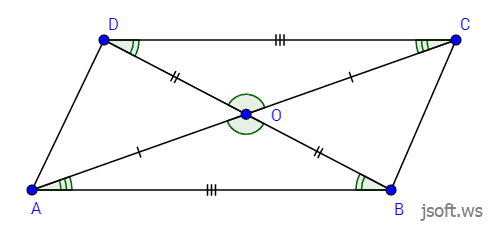
Paraleloqram

Paraleloqramın qarşı tərəfləri bərabərdir, qarşı bucaqları bərabərdir, bir tərəfə söykənən bucaqlarının cəmi 180°-yə bərabərdir. Paraleloqramın diaqonalları kəsişmə nöqtəsində yarı bölünür.

Tebo teoremləri

Paraleloqramın tərəfləri üzərində qurulmuş kvadratların mərkəzləri özü, kvadratın təpə nöqtələridir. Əgər kvadratın iki qonşu tərəfində bərabərtərəfli üçbucaq qursaq bu üçbucaqların kvadrata aid olmayan təpələri ilə kvadratın bu üçbucaqlara aid olmayan təpəsini birləşdirərkən bərabərtərəfli üçbucaq alarıq.

Trapesiya

Yalnız iki qarşı tərəfi paralel olan qabarıq dördbucaqlıya trapesiya deyilir. Bu paralel tərəflərə trapesiyanın oturacaqları, paralel olmayan tərəflərə isə yan tərəfləri deyilir. Trapesiyanın qarşı təpələrini birləşdirən düz xətt parçasına onun diaqonalı deyilir.

Dördbucaqlı üçün Van-Obel teoremi

İxtiyarı dördbucaqlının tərəflərində xarici kvadratlar qursaq, qarşılıqlı kvadratların orta nöqtələrini birləşdirən düz xətt parçaları bərabər və perpendikulyar olacaq.

Varinyon teoremi

İstənilən dördbucaqlının tərəflərinin orta nöqtəsini birləşdirsək paraleloqram alarıq. Bu teoremdə dördbucaqlının qabarıq olması şərt deyil və bütün dördbucaqlılar üçün doğrudur.

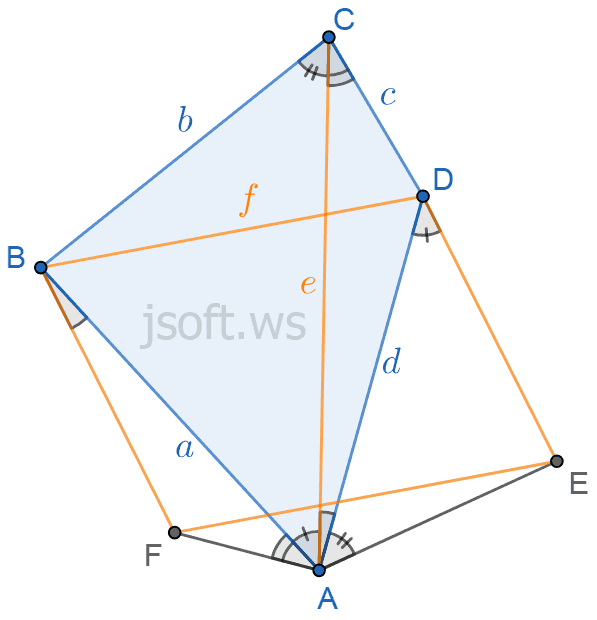
Bretşnayder teoremi

Bretşnayder teoreminə bəzi mənbələrdə Bretşnayder münasibəti də deyilir. Əslində bu teoremi dördbucaqlı üçün kosinuslar teoremi adlandırmaq olar. Həmin teoremin isbatını bu məqalədə oxuya bilərsiniz.

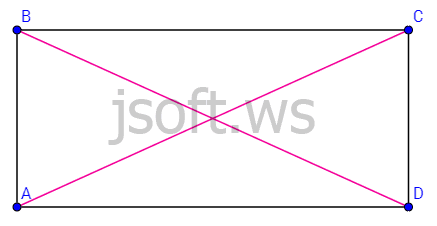
Düzbucaqlı, romb, kvadrat

Bütün bucaqları düz bucaq olan paraleloqrama düzbucaqlı deyilir. Bütün tərəfləri bərabər olan paraleloqrama romb deyilir. Bütün tərəfləri bərabər olan düzbucaqlı kvadrat adlanır.

Üçbucaq daxilinə çəkilmiş kvadrat

Əgər kvadratın tərəfi üçbucağın bir tərəfində yerləşib digər iki təpəsi üçbucağın digər tərəfləri üzərindədirsə bu kvadrat üçbucaq daxilinə çəkilmiş kvadrat adlanır. Üçbucaq daxilinə çəkilmiş kvadratın tərəfi bu üçbucağın oturacağı ilə hündürlüyü hasilinin, həmin oturacaq ilə həmin hündürlük cəminə nisbətinə bərabərdir.

Düzbucaqlının sahəsi

Düzbucaqlının sahəsi onun tərəflərinin hasilinə bərabərdir. Düzbucaqlının sahəsi onun xaricinə çəkilmiş çevrənin radiusu kvadratının, düzbucaqlının diaqonalları arasındakı bucağın sinusuna hasilinin iki mislinə bərabərdir.

Rombun sahəsi

Romb paraleloqramın xüsusi hali olduğu üçün paraleloqramın sahə düsturları burada da keçərlidir. Rombun sahəsi daxilinə çəkilmiş çevrənin diametrinin onun tərəfinə hasilinə bərabərdir. Bundan başqa bu sahə daxilə çəkilmiş çevrənin diametrinin iki tərəf arasındakı bucağın sinusina nisbətinə bərabərdir.

Paraleloqramın sahəsi

Paraleloqramın sahəsi onun oturacağı ilə hündürlüyü hasilinə bərabərdir. Paraleloqramın sahəsi onun iki tərəfi ilə bu tərəflər arasında qalan bucağın sinusu hasilinə bərabərdir. Paraleloqramın sahəsi onun diaqonalları və bu diaqonallar arasında qalan bucağın sinusu hasilinin yarısına bərabərdir.

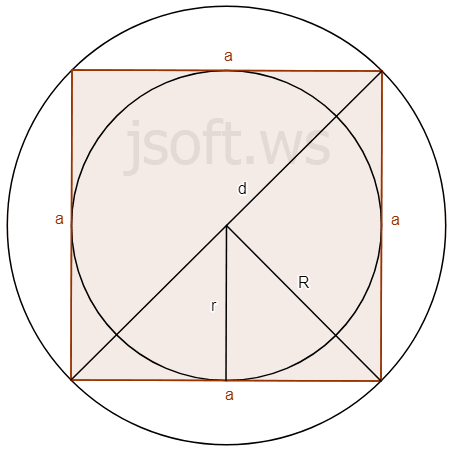
Kvadratın sahəsi

Kvadratın sahəsi daxilinə çəkilmiş çevrənin radiusu kvadratının dörd mislinə bərabərdir. Bu sahə həmçinin onun diaqonalının kvadratının yarısına bərabərdir. Kvadratın sahəsi onun xaricinə çəkilmiş çevrənin radiusu kvadratının iki mislinə bərabərdir.

Trapesiyanın sahəsi

Trapesiyanın sahəsi oturacaqlarının cəmini yarısı ilə hündürlüyü hasilinə bərabərdir. Bu sahəni trapesiyanın diaqonalları ilə bu diaqonalların kəsişməsindən alınan bucağın sinusu hasilinin yarısı kimi də ifadə etmək olar.

Sadə fiqurların sahəsi

Üçbucaq, düzbucaqlı, trapesiya, paraleloqram və rombun sahə düsturları yəqin ki, məktəb kursundan yadınızdadır. Bəs bu sahə düsturlarının çıxarılışı necə? O da yadınızadadırmı? Əgər unutmusunuzsa oxuyub hamısını bir dəfəyə yada salın.