Ana səhifə :: Riyaziyyat :: Həndəsə :: Vektorlar
Yaranma tarixi:
Vektorların toplanması
vektor
Vektorların toplanması üçün üçbucaq qaydası

Şəkil 1
Tutaq ki, hər hansı nöqtə əvvəl $A$ nöqtəsindən $B$ nöqtəsinə, sonra isə $B$ nöqtəsindən $C$ nöqtəsinə düz xətt üzrə hərəkət edib. Bu iki yerdəyişmə nəticəsində nöqtə $A$ nöqtəsindən $C$ nöqtəsinə keçib. Ona görə son yerdəyişməni $\overrightarrow {AC}$ vektoru göstərir. Həmin $\overrightarrow {AC}$ yerdəyişməsi $\overrightarrow {AB}$ və $\overrightarrow {BC}$ vektorlarının cəmindən alındığı üçün onu aşağıdakı kimi göstərmək olar.
$\overrightarrow {AC} = \overrightarrow {AB} +\overrightarrow{BC}$
İndi vektorların toplanmasının tərifini verək. Tutaq ki, $\vec {a}$ və $\vec {b}$ vektorları verilib. Müstəvinin $A$ nöqtəsindən $\vec {a}$-ya bərabər olan $\overrightarrow {AB}$, $B$ nöqtəsindən isə $\vec {b}$-yə bərabər olan $\overrightarrow {BC}$ vektorunu çəkək. Onda $\overrightarrow {AC}$ vektoru $\vec {a}$ və $\vec {b}$ vektorlarının cəmi adlanır və $\vec{a}+\vec{b}$ kimi işarə edilir.
Bu cür toplanma vektorların toplanmasının üçbucaq qaydası adlanır.
Şəkil 2
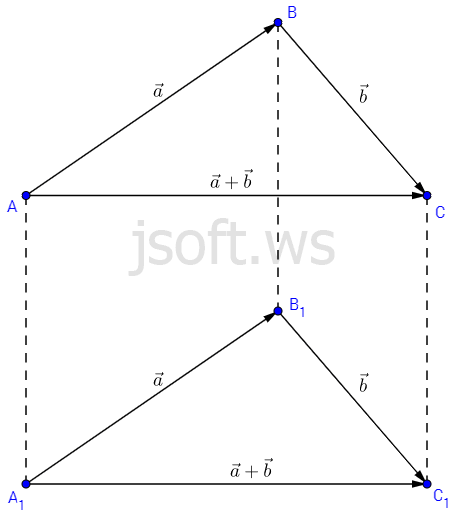
Göstərək ki, bu cür toplama zamanı $A$ nöqtəsinin harada seçilməsi nəticəyə təsir etmir. Yəni, $A$ əvəzinə hər hansı $A_1$ nöqtəsi seçsək $\overrightarrow {AB} = \overrightarrow {A_1B_1}$, $\overrightarrow {BC}=\overrightarrow {B_1C_1}$ olarsa $\overrightarrow {AC}=\overrightarrow {A_1C_1}$ olacaq.
Indi isə Şəkil 2-yə baxın. $\overrightarrow {AB} = \overrightarrow {A_1B_1}$ o deməkdir ki, $ABB_1A_1$ dördbucaqlısının iki qarşı tərəfi paralel və bərabərdir. Deməli, bu dördbucaqlı paraleloqramdır. Yəni $\overrightarrow {AA_1} = \overrightarrow {BB_1}$. Eynilə $BCC_1B_1$ dördbucaqlısı da paraleloqram olduğu üçün $\overrightarrow {BB_1} = \overrightarrow {CC_1}$. Yəni $\overrightarrow {AA_1} = \overrightarrow {CC_1}$ və $ACC_1A_1$ də paraleloqramdır.
Biz aldıq ki, $\overrightarrow {AC} = \overrightarrow {A_1C_1}$
İstənilən $\vec {a}$ üçün $\vec {a} + \vec {0} = \vec {a}$.
Vektorların üçbucaq qaydası ilə toplanmasından bu nəticə çıxır.
Nəticə: $A$, $B$ və $C$ müstəvidə istənilən nöqtələrdirsə, $\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC}$ həmişə doğrudur.
Vektorların toplanması üçün paraleloqram qaydası
Teorem: İxtiyari $\vec {a}$, $\vec {b}$ və $\vec {c}$ üçün aşağıdakı bərabərliklər doğrudur.
1. $\vec {a} +\vec {b} = \vec {b} +\vec {a}$ – kommutativlik şərti
2. $(\vec {a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$ – assosiativlik şərti
İsbatı:

Şəkil 3
1. $\vec {a}$ və $\vec {b}$ vektorlarının kollinear olmadığı halı araşdıraq. Kollinear olan hal trivialdır. İstənilən $A$ nöqtəsindən $\overrightarrow {AB}=\vec{a}$ və $\overrightarrow {AD}=\vec {b}$ vektorları çəkək. Bu vektorlar üzərində paraleloqram quraq (Şəkil 3). Vektorların toplanmasının üçbucaq qaydasına görə
$\overrightarrow {AC} = \overrightarrow {AB}+\overrightarrow {BC} = \vec {a}+\vec{b}\\
\overrightarrow{AC}=\overrightarrow{AD}+\overrightarrow{DC}=\vec{b}+\vec{a}$
Deməli, $\vec {a}+\vec{b} = \vec {b}+\vec{a}$.

Şəkil 4
2. Müstəvidə ixtiyari $A$ nöqtəsi götürüb həmin nöqtədən $\overrightarrow {AB} = \vec {a}$, $B$ nöqtəsindən $\overrightarrow {BC}=\vec{b}$, $C$ nöqtəsindən isə $\overrightarrow {CD}=\vec {c}$ çəkək (Şəkil 4). Üçbucaq qaydası ilə ardıcıl $\vec {a}$, $\vec{b}$ və $\vec {c}$ vektorlarını toplasaq aşağıdakını alaraq.
$(\vec{a}+\vec{b})+\vec{c}=(\overrightarrow {AB}+\overrightarrow{BC})+\overrightarrow{CD} = \overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}\\
\vec{a}+(\vec{b}+\vec{c}) = \overrightarrow{AB}+(\overrightarrow{BC}+\overrightarrow{CD})=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}$
Hər iki halda $\overrightarrow{AD}$ vektorunu aldıq. Yəni $(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$
Bu teoremin isbatının birinci hissəsində vektorları toplamaq üçün daha bir qayda verdik. Bu qaydaya vektorların toplanması üçün paraleloqram qaydası deyilir. Kollinear olmayan $\vec {a}$ və $\vec{b}$ vektorlarını toplamaq üçün $A$ nöqtəsindən $\overrightarrow {AB}=\vec{a}$ və $\overrightarrow {AD}=\vec{b}$ ayırıb $ABCD$ paraleloqramı qurmaq lazımdır. Onda həmin paraleloqramın $\overrightarrow{AC}$ diaqonalı bizə lazım olan vektor olacaq, $\overrightarrow {AC}=\vec{a}+\vec{b}$.
Paraleloqram qaydası əsasən fizikada qüvvələri toplamaq üçün istifadə olunur.
Bir neçə vektorun toplanması belə həyata keçirilir. Əvvəl birinci vektor ikinci ilə toplanır, alınmış vektor üçüncü ilə toplanır, və s. İsbat etdik ki, bu cür toplama zamanı ardıcıllıq əhəmiyyət kəsb etmir. Bu cür toplama çoxbucaqlı qaydası adlanır.
Nəticə: Müstəvidə istənilən qaydada verilmiş $A_1$, $A_2$, …, $A_n$ nöqtələri üçün $\overrightarrow {A_1A_2} + \overrightarrow{A_2A_3} + ... +\overrightarrow {A_{n-1}A_n} = \overrightarrow {A_1A_n}$. Əgər $A_1=A_n$ olarsa bu vektorların cəmi $\vec {0}$ olacaq.
Digər məqalələr

Vektor nədir?
Başlanğıcı və sonu olan istiqamətlənmiş düz xətt parçasına vektor deyilir. Əgər iki vektor perpendikulyar düz xətlər üzərində yerləşibsə onlara ortoqonal, bir düz xətt və ya paralel düz xətlər üzərində yerləşibsə, onlara kollinear vektorlar deyilir.

Vektorların çıxılması
İki vektorun fərqi elə bir vektordur ki, onun üzərinə çıxılan vektoru gəlsək azalan vektoru alarıq. İstənilən a və b vektoru üçün a-b=a+(-b) bərabərliyi doğrudur.

Vektorların skalyar hasili
İki vektorun skalyar hasili onların uzunluğu ilə aralarındakı bucağın kosinusunun hasilinə bərabərdir. Həmçinin iki vektorun skalyar hasili onların uyğun koordinatlarının hasili cəminə bərabərdir.

Vektorun koordinatları
Bərabər vektorların uyğun koordinatları bərabərdir. Uyğun koordinatları bərabər olan vektorlar bərabərdir. İki və daha çox vektorun cəminin koordinatları onların uyğun koordinatları cəminə bərabərdir. Vektorun ədədə hasilinin hər bir koordinatı, uyğun koordinatın həmin ədədə hasilinə bərabərdir.

Vektorun ədədə vurulması
Sıfırdan fərqli olan a vektorunun k ədədinə hasili elə b vektoruna deyilir ki, onun uzunluğu |b|=|k||a| olsun. b vektorunun istiqaməti isə k>0 olarsa a ilə eyni, k<0 olarsa a-nın əksinə olacaq.
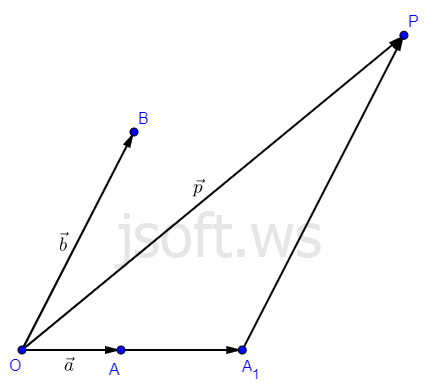
Vektorun iki kollinear olmayan vektora ayrılışı
Əgər a və b vektorları kollineardırsa və a vektoru b-dən fərqlidirsə, onda elə k ədədi var ki, b=ka. Müstəvidə verilmiş istənilən vektoru kollinear olmayan iki vektorun ayrılışı şəklində göstərmək olar və bu ayrılış yeganədir.
© Müəllif hüquqları qorunur
Bu saytdakı bütün məqalələr Cəfər N.Əliyev tərəfindən yazılıb. Onlar hər hansı üçüncu şəxs tərəfindən digər resurslarda çap edilərsə mənbə və müəllifin adı göstərilməlidir. Sayt özü həmin şərtlərə əməl edir.
