Yaranma tarixi: 26 Yanvar, 2018

Vektorun iki kollinear olmayan vektora ayrılışı

Lemma: Əgər $\vec{a}$ və $\vec{b}$ kollineardırsa və $\vec{a}\ne\vec{0}$, onda elə $k$ ədədi var ki, $\vec{b}=k\vec{a}$.

İsbatı: $\vec{a}$ və $\vec{b}$ vektorlarının eyni istiqamətli ($\vec{a} \uparrow \uparrow \vec{b}$) və əks istiqamətli ($\vec{a} \uparrow \downarrow \vec{b}$) olduğu hallara ayrılıqda baxacağıq.

I hal.  $\vec{a} \uparrow \uparrow \vec{b}$

Bu hal üçün $k=\dfrac{|\vec{b}|}{|\vec{a}|}$ götürsək, $k \geqslant 0$ olduğu üçün $k\vec{a}$ və $\vec{b}$ vektorları eyni istiqamətlidir və onların uzunluqları eynidir. Onda vektorun ədədə vurulmasının tərifinə görə

$|k\vec{a}|=|k||\vec{a}|=\dfrac{|\vec{b}|}{|\vec{a}|} |\vec{a}|=|\vec{b}|$

Yəni, $\vec{b}=k\vec{a}$

II hal.  $\vec{a} \uparrow \downarrow \vec{b}$

Bu hal üçün $k=-\dfrac{|\vec{b}|}{|\vec{a}|}$ götürək. $k<0$ olduğu üçün $k\vec{a}$ vektoru $\vec{a}$ vektoru ilə əks istiqamətli, yəni $\vec{b}$ vektoru ilə eyni istiqamətli olacaq. Uzunluqları da yuxarıdakı düstura görə bərabərdir. Yenə də $\vec{b}=k\vec{a}$.

Lemma isbat olundu.

Tutaq ki, $\vec{a}$ və $\vec{b}$ vektorları verilib. Əgər hər hansı $\vec{p}$ vektoru $\vec{p}=x \vec{a}+y\vec{b}$ şəklində verilərsə ($x$ və $y$ hər hansı ədədlərdir), onda bu yazılışa $\vec{p}$ vektorunun $\vec{a}$ və $\vec{b}$ üzrə ayrılışı deyilir. $x$ və $y$ bu ayrılışın əmsalları adlanır.

Teorem: Müstəvidə verilmiş istənilən vektoru kollinear olmayan iki vektorun ayrılışı şəklində göstərmək olar və bu ayrılış yeganədir.

İsbatı: Tutaq ki, $\vec{a}$ və $\vec{b}$ kollinear olmayan vektorlardır. Əvvəlcə isbat edək ki, istənilən $\vec{p}$ vektorunu $\vec{a}$ və $\vec{b}$ üzrə ayırmaq olar. İki hal mümkündür.

I hal. $\vec{p}$ vektoru $\vec{a}$ və ya $\vec{b}$ ilə kollineardır. Tutaq ki, bu vektor $\vec{b}$-dir. Onda yuxarıdakı lemmaya görə $\vec{p}=k\vec{b}$ yazmaq olar. Tam yazsaq

$\vec{p}=0\cdot \vec{a} + y\cdot \vec{b}$

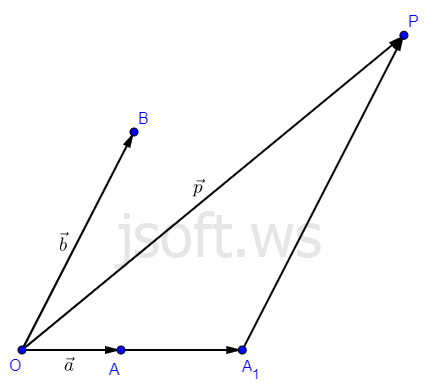
II hal. $\vec{p}$ heç bir vektora kollinear deyil. Müstəvidə bir $O$ nöqtəsi götürüb hər üç vektorun başlanğıcını həmin nöqtəyə paralel köçürək. $\overrightarrow{OA}=\vec{a}$, $\overrightarrow{OB}=\vec{b}$, $\overrightarrow{OP}=\vec{p}$. $P$ nöqtəsindən $OB$ xəttinə paralel düz xətt çəksək və onun $OA$ düz xətti ilə kəsişməsini $A_1$ nöqtəsi ilə işarə etsək vektorların toplanmasının üçbucaq qaydasına görə

$\vec{p}=\overrightarrow{OA_1}+\overrightarrow{A_1P}$.

$\overrightarrow{OA_1}$ vektoru $\overrightarrow{OA}$ ilə, $\overrightarrow{A_1P}$ vektoru isə $\overrightarrow{OB}$ ilə kollinear olduğu üçün elə $x$ və $y$ ədədləri var ki

$\overrightarrow{OA_1} = x \cdot \overrightarrow{OA} = x\vec{a}$, $\overrightarrow{A_1P}=y\cdot \overrightarrow{OB}=y \vec{b}$

Deməli, $\vec{p}=x\vec{a}+y\vec{b}$.

İndi yeganəliyi isbat edək. Tutaq ki, $\vec{p}=x\vec{a}+y\vec{b}$ və başqa hər hansı $x_1$ və $y_1$ əmsalları da var ki, $\vec{p}=x_1\vec{a}+y_1\vec{b}$ doğrudur. Bu bərabərlikləri çıxsaq

$\vec{0} = (x-x_1)\vec{a} +(y-y_1)\vec{b}$

alarıq. Yuxarıdakı bərabərlik yalnız o zaman doğru olar ki, $x-x_1$ və $y-y_1$ fərqlərinin hər ikisi sıfıra bərabər olsun. Əks hala baxaq. Tutaq ki, $x-x_1 \ne 0$. Onda yuxarıdakı tənliyi $x-x_1$-ə görə həll etsək

$\vec{a}=-\dfrac{y-y_1}{x-x_1} \vec{b}$

alarıq. Bu isə $\vec{a}$ və $\vec{b}$-nin kollinearlığı deməkdir. Biz ziddiyyətə gəldik. Çünki teoremin şərtində deyilir ki, bu vektorlar kollinear deyil. Eynilə $y-y_1 \ne 0$ da ola bilməz. Deməli, $x=x_1$ və $y=y_1$, yəni ayrılış əmsalları yeganədir.

Digər məqalələr

Vektor nədir?

Başlanğıcı və sonu olan istiqamətlənmiş düz xətt parçasına vektor deyilir. Əgər iki vektor perpendikulyar düz xətlər üzərində yerləşibsə onlara ortoqonal, bir düz xətt və ya paralel düz xətlər üzərində yerləşibsə, onlara kollinear vektorlar deyilir.

Vektorların çıxılması

İki vektorun fərqi elə bir vektordur ki, onun üzərinə çıxılan vektoru gəlsək azalan vektoru alarıq. İstənilən a və b vektoru üçün a-b=a+(-b) bərabərliyi doğrudur.

Vektorların toplanması

İki vektoru üçbucaq və paraleloqram qaydası ilə toplamaq olar. İstənilən a, b, və c vektoru üçün a+b=b+a kommutativlik və (a+b)+c=a+(b+c) assosiativlik qaydaları doğrudur.

Vektorların skalyar hasili

İki vektorun skalyar hasili onların uzunluğu ilə aralarındakı bucağın kosinusunun hasilinə bərabərdir. Həmçinin iki vektorun skalyar hasili onların uyğun koordinatlarının hasili cəminə bərabərdir.

Vektorun koordinatları

Bərabər vektorların uyğun koordinatları bərabərdir. Uyğun koordinatları bərabər olan vektorlar bərabərdir. İki və daha çox vektorun cəminin koordinatları onların uyğun koordinatları cəminə bərabərdir. Vektorun ədədə hasilinin hər bir koordinatı, uyğun koordinatın həmin ədədə hasilinə bərabərdir.

Vektorun ədədə vurulması

Sıfırdan fərqli olan a vektorunun k ədədinə hasili elə b vektoruna deyilir ki, onun uzunluğu |b|=|k||a| olsun. b vektorunun istiqaməti isə k>0 olarsa a ilə eyni, k<0 olarsa a-nın əksinə olacaq.