Ana səhifə :: Riyaziyyat :: Həndəsə :: Vektorlar
Yaranma tarixi:
Vektorun koordinatları
vektor koordinat

Əgər $\vec{a}$ vektorunun başlanğıcı $A_1(x_1;y_1)$, sonu $A_2(x_2;y_2)$ nöqtəsindədirsə, bu vektorun koordinatları $a_1=x_2-x_1$ və $a_2=y_2-y_1$ olacaq. Bu zaman $\vec{a}$ vektoru $\overrightarrow {(a_1;a_2)}$ və ya $\vec{a}(a_1;a_2)$ kimi işarə edilir. $\vec{0}$ vektorunun koordinatları sıfıra bərabər olduğu üçün $\vec{0}(0;0)$ kimi göstərilir.
$\vec{a}$ vektorunun dekart koordinat sistemində təsvirinə baxsaq görərik ki, koordinatı $(a_1; a_2)$ olan vektorun uzunluğu Pifaqor teoreminə görə $\sqrt{a_1^2+a_2^2}$ olacaq.
Teorem 1: Bərabər vektorların uyğun koordinatları bərabərdir. Uyğun koordinatları bərabər olan vektorlar bərabərdir.
İsbatı: Tutaq ki, $A_1(x_1;y_1)$ və $A_2(x_2;y_2)$ nöqtələri $\vec{a}$ vektorunun başlanğıc və son nöqtələridir. $\vec{a’}=\vec{a}$ olan hər hansı $\vec{a’}$ vektoru paralel köçürmə ilə alındığı üçün onun başlanğıc və son koordinatları uyğun olaraq $A_1’(x_1+c; y_1+d)$ və $A_2’(x_2+c; y_2+d)$ olacaq. Bu koordinatları bir-birindən çıxanda $\vec{a}$ və $\vec{a’}$ üçün eyni $(x_2-x_1; y_2-y_1)$ koordinatları alarıq.
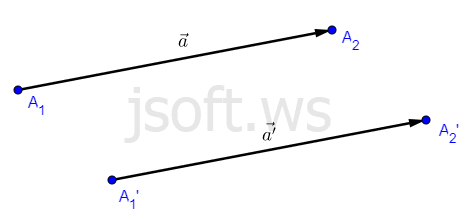
İndi tərsini isbat edək. Tutaq ki, $\vec{a}$ və $\vec{a’}$ vektorlarının uyğun koordinatları bərabərdir. Teoremin şərtinə görə $a_1=a_1’$ və $a_2=a_2’$. Deməli,
$x_2-x_1=x_2’-x_1’ , \ y_2-y_1=y_2’-y_1’ \Rightarrow x_2’ = x_2+x_1’-x_1,\ y_2’ = y_2+y_1’-y_1$
Onda aşağıdakı düsturla verilmiş paralel köçürmə $A_1$ nöqtəsini $A_1’$-ə, $A_2$ nöqtəsini $A_2’$-ə çevirir. Yəni, $\overrightarrow {A_1A_2}=\overrightarrow {A_1’A_2’}$.
$x’=x+x_1’-x_1, \ y’=y+y_1’-y_1$
Teorem isbat olundu.
Vektorun koordinatlarını taparkən həmişə son nöqtəsinin koordinatlarından başlanğıc nöqtənin koordinatlarını çıxdığımıza görə vektoru həmişə koordinat başlanğıcından çəkə bilərik. $x$ və $y$ oxları üzrə vahid vektorları uyğun olaraq $\vec{i}$ və $\vec{j}$ ilə işarə etsək, vektorların ayrılışı teoreminə görə istənilən $\vec{p}$ vektorunu $\vec{p}=x\vec{i}+y\vec{j}$ kimi göstərə bilərik və bu ayrılış yeganədir.
Teorem 2: İki və daha çox vektorun cəminin koordinatları onların uyğun koordinatları cəminə bərabərdir.
İsbatı: Bunu iki vektor halı üçün isbat edək. $\vec{a} = x_1\vec{i}+y_1\vec{j}$ və $\vec{b}=x_2\vec{i}+y_2\vec{j}$ vektorlarına baxsaq vektorun ədədə vurulmasının I paylama qanununa görə
$\vec{a}+\vec{b}=x_1\vec{i}+y_1\vec{j}+ x_2\vec{i}+y_2\vec{j}=(x_1+x_2)\vec{i}+(y_1+y_2)\vec{j}$
Yəni $\vec{a}+\vec{b}$ vektorunun koordinatları $(x_1+x_2; y_1+y_2)$ olacaq.
Teorem 3: İki vektorun fəqqinin koordinatları onların uyğun koordinatları fərqinə bərabərdir.
İsbatı: Bu teorem də eynilə yuxarıdakı kimi isbat edilir.
$\vec{a}-\vec{b}=x_1\vec{i}+y_1\vec{j}-x_2\vec{i}-y_2\vec{j} = (x_1-x_2)\vec{i}+(y_1-y_2)\vec{j}$
Yəni $\vec{a}-\vec{b}$ vektorunun koordinatları $(x_1-x_2; y_1-y_2)$ olacaq.
Teorem 4: Vektorun ədədə hasilinin hər bir koordinatı, uyğun koordinatın həmin ədədə hasilinə bərabərdir.
İsbatı: Tutaq ki, $\vec{a}(x; y)$ vektoru verilib. Onda
$k\vec{a} = k(x\vec{i}+y\vec{j})=kx\vec{i}+ky\vec{j}$
Yəni $k\vec{a}$ vektorunun kordinatları $(kx; ky)$-dir.
Digər məqalələr

Vektor nədir?
Başlanğıcı və sonu olan istiqamətlənmiş düz xətt parçasına vektor deyilir. Əgər iki vektor perpendikulyar düz xətlər üzərində yerləşibsə onlara ortoqonal, bir düz xətt və ya paralel düz xətlər üzərində yerləşibsə, onlara kollinear vektorlar deyilir.

Vektorların çıxılması
İki vektorun fərqi elə bir vektordur ki, onun üzərinə çıxılan vektoru gəlsək azalan vektoru alarıq. İstənilən a və b vektoru üçün a-b=a+(-b) bərabərliyi doğrudur.

Vektorların toplanması
İki vektoru üçbucaq və paraleloqram qaydası ilə toplamaq olar. İstənilən a, b, və c vektoru üçün a+b=b+a kommutativlik və (a+b)+c=a+(b+c) assosiativlik qaydaları doğrudur.

Vektorların skalyar hasili
İki vektorun skalyar hasili onların uzunluğu ilə aralarındakı bucağın kosinusunun hasilinə bərabərdir. Həmçinin iki vektorun skalyar hasili onların uyğun koordinatlarının hasili cəminə bərabərdir.

Vektorun ədədə vurulması
Sıfırdan fərqli olan a vektorunun k ədədinə hasili elə b vektoruna deyilir ki, onun uzunluğu |b|=|k||a| olsun. b vektorunun istiqaməti isə k>0 olarsa a ilə eyni, k<0 olarsa a-nın əksinə olacaq.
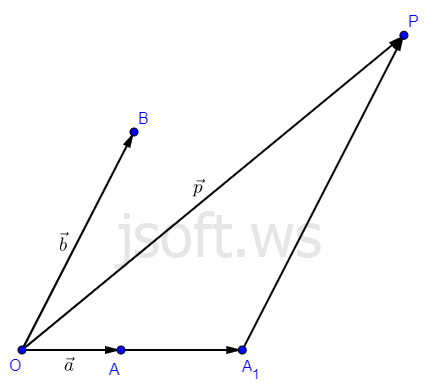
Vektorun iki kollinear olmayan vektora ayrılışı
Əgər a və b vektorları kollineardırsa və a vektoru b-dən fərqlidirsə, onda elə k ədədi var ki, b=ka. Müstəvidə verilmiş istənilən vektoru kollinear olmayan iki vektorun ayrılışı şəklində göstərmək olar və bu ayrılış yeganədir.
© Müəllif hüquqları qorunur
Bu saytdakı bütün məqalələr Cəfər N.Əliyev tərəfindən yazılıb. Onlar hər hansı üçüncu şəxs tərəfindən digər resurslarda çap edilərsə mənbə və müəllifin adı göstərilməlidir. Sayt özü həmin şərtlərə əməl edir.
