Bu teq üzrə məqalələr: 'çevrə'

Ptolemey teoremi
Çevrə daxilinə çəkilmiş dördbucaqlının diaqonallarının hasili qarşı tərəflərin hasilləri cəminə bərabərdir.

Çevrə və bucaqların 6 xassəsi
Kəsişən vətərlər arasındakı bucaq həmin bucağın tərəfləri arasında qalan qövslərin ölçüləri cəminin yarısına bərabərdir. Çevrəni kəsən iki düz xətt arasındakı bucaq, həmin bucağın kəsişmədə əmələ gətirdiyi böyük qövs ilə kiçik qövsün fərqinin yarısına bərabərdir.

Brahmaqupta teoremi
Çevrə daxilinə çəkilmiş dördbucaqlının sahəsi bu dördbucaqlının yarım perimetri ilə tərəfləri fərqinin hasilinin kvadrat kökünə bərabərdir.

Kəpənək teoremi
Tutaq ki, M nöqtəsi çevrənin PQ vətərinin orta nöqtəsidir. Həmin M nöqtəsindən iki AB və CD vətərləri çəkək. AD parçasının PQ vətərini kəsən nöqtəni X, BC parçasının PQ vətərini kəsən nöqtəni Y ilə işarə edək. Onda M nöqtəsi XY parçasının da orta nöqtəsi olacaq.
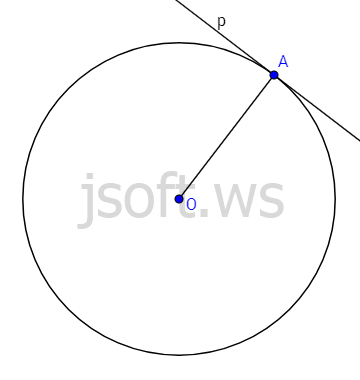
Çevrəyə toxunan
Əgər çevrə və düz xəttin yalnız bir orta nöqtəsi varsa bu düz xəttə çevrəyə toxunan deyilir.Çevrəyə toxunan, toxunma nöqtəsindən çəkilmiş radiusa perpendikulyardır.

Nagel nöqtəsi
Üçbucağın tərəflərinə xaricdən daxilə çəkilmiş çevrələrin bu tərəflərə toxunma nöqtələrini qarşı təpələrlə birləşdirən çevianların kəsişmə nöqtəsiə üçbucağın Nagel nöqtəsi deyilir. Nagel nöqtəsinin varlığı Çeva teoreminin köməyi ilə isbat edilir.

Karno düsturu
İtibucaqlı üçbucağın xaricinə çəkilmiş çevrənin mərkəzindən onun tərəflərinə qədər olan məsafələrin cəmi, həmin üçbucağın daxilinə və xaricinə çəkilmiş çevrələrin radiusları cəminə bərabərdir. Bu düstur Fransız riyazıyyatçısı, hərbi mühəndis və dövlət xadimi, Lazar Karnonun adı ilə bağlıdır.

Çevrə və Dairə
Müstəvidə verilmiş nöqtədən eyni məsafədə olan nöqtələrin əmələ gətirdiyi həndəsi fiqura çevrə deyilir. Müstəvinin çevrə ilə məhdudlaşmış hissəsinə dairə edilir.
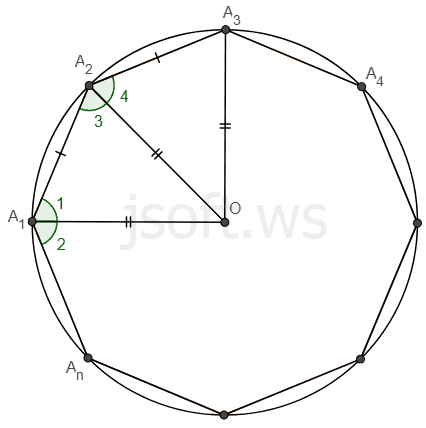
Düzgün çoxbucaqlının xaricinə və daxilinə çəkilmiş çevrələr
Əgər çoxbucaqlının bütün təpələri çevrə üzərindədirsə, bu çevrəyə çoxbucaqlının xaricinə çəkilmiş çevrə deyilir. Əgər çoxbucaqlının bütün tərəfləri çevrəyə toxunursa, bu çevrəyə çoxbucaqlı daxilinə çəkilmiş çevrə deyilir. İstənilən düzgün çoxbucaqlının xaricinə və daxilinə həmişə çevrə çəkmək olar.

Xaricdən daxilə çəkilmiş çevrə
Üçbucağın xaricindən daxilə çəkilmiş çevrə (və ya xaricdən daxilə çəkilmiş çevrə) elə çevrədir ki, üçbucağın bir tərəfinə xaricdən toxunur, digər iki tərəfin isə uzantılarına toxunur. Xaricdə daxilə çəkilmiş çevrənin mərkəzi toxunduğu tərəfin qarşısındakı daxili bucağının tənböləni ilə digər iki xarici bucağın tənbölənlərinin kəsişmə nöqtəsidir.

Üçbucağın xaricinə və daxilinə çəkilmiş çevrələr
Əgər çevrə üçbucağın bütün təpələrindən keçirsə, onda bu çevrə üçbucaq xaricinə çəkilmiş çevrə adlanır. Çevrə üçbucağın bütün tərəflərinə toxunursa, onda ona üçbucaq daxilin çəkilmiş çevrə deyilir. İstənilən üçbucağın xaricinə və daxilinə yeganə çevrə çəkmək olar.

Çevrə uzunluğu və dairənin sahəsi
Çevrə uzunluğunu və dairənin sahəsini tapmaq üçün onun daxilinə və xaricinə düzgün 6-bucaqlı çəkək. Daxilə çəkilmiş 6-bucaqlının perimetri p, sahəsi isə s, xaricə çəkilmiş 6-bucaqlını perimetri P, sahəsi isə S olsun.

Çevrə vətərinin 9 xassəsi
Çevrənin mərkəzindən eyni məsafədə olan vətərlər bərabərdir. Əgər vətərlər bərabər mərkəzi bucaqlar qarşısındadırsa onlar bərabərdir. Əgər diametr vətərə perpendikulyardırsa onun mərkəzindən keçir. Eyni vətərə eyni tərəfdən söykənən daxili bucaqlar bərabər, müxtəlif tərəflərdən söykənən bucaqların cəmi 180°-yə bərabərdir.

Dördbucağın xaricinə və daxilinə çəkilmiş çevrələr
Çevrə daxilinə çəkilmiş istənilən dördbucaqlının qarşı bucaqlarının cəmi 180°-yə bərabərdir. Çevrə xaricinə çəkilmiş istənilən dördbucaqlının qarşı tərəflərinin cəmi bərabərdir.

Daxilə çəkilmiş və mərkəzi bucaqlar
Təpəsi çevrənin mərkəzində olan bucağa mərkəzi bucaq deyilir. Təpəsi çevrə üzərində olub tərəfləri çevrənin tərəflərini kəsən bucağa daxili bucaq deyilir. Daxili bucaq söykəndiyi qövsün yarısı ilə ölçülür.
