Yaranma tarixi: 26 Yanvar, 2019

Oxşar üçbucaqların xassələri

oxşar üçbucaq oxşarlıq xassə

 

Oxşar üçbucaqların aşağıdakı xassələri var.

Xassə 1: Oxşar üçbucaqların sahələrinin nisbəti onların oxşarlıq əmsalının kvadratına bərabərdir.

$\dfrac{S}{S_1} = k^2$

Burada $S$, $ABC$ üçbucağının, $S_1$ isə $A_1B_1C_1$ üçbucağının sahəsidir. Bu xasəni artıq üçbucağın sahəsinin xassələri məqaləsində isbat etmişik.

Xassə 2: Oxşar üçbucaqların perimetrlərinin nisbəti onların oxşarlıq əmsalına bərabərdir.

İsbatı: $\triangle ABC \sim \triangle A_1B_1C_1$. Bu isə o deməkdir ki,

$\dfrac{AB}{A_1B_1} = \dfrac{BC}{B_1C_1} = \dfrac{AC}{A_1C_1}= k$

Bur nisbətlərdən $AB$, $BC$ və $AC$-ni tapaq.

$AB= k \cdot A_1B_1; \ BC = k \cdot B_1C_1; \ AC = k \cdot A_1C_1$

Indi perimetrlərin nisbətinə baxaq.

$\dfrac {AB+BC+AC}{ A_1B_1+B_1C_1+A_1C_1 } =\\[15pt]
= \dfrac{ k \cdot A_1B_1+ k \cdot B_1C_1+k \cdot A_1C_1}{ A_1B_1+B_1C_1+A_1C_1} =\\[15pt]
= \dfrac{ k \cdot (A_1B_1+B_1C_1+A_1C_1)}{ A_1B_1+B_1C_1+A_1C_1} =k$

Xassə isbat olundu.

Xassə 3: Oxşar üçbucaqların uyğun tənbölənlərinin, medianlarının, hündürlüklərinin, daxillərinə və xariclərinə çəkilmiş çevrələrin radiuslarının nisbəti onların oxşarlıq əmsalına bərabərdir. Bu deyilənləri ümumiləşdirərək deyirlər ki, oxşar üçbucaqlarının xətti elementlərinin nisbəti üçbucaqların oxşarlıq əmsalına bərabərdir.

İsbatı: Tutaq ki, $ABC$ və $A_1B_1C_1$ oxşar üçbucaqlarının uyğun tərəflərinin nisbətləri $k$-ya bərabərdir. Tənbölənlərin mütənasibliyini isbat etmək üçün $C$ və $C_1$ bucaqlarının tənbölənlərini çəkək. Bu zaman alınan $\triangle ACD$ və $\triangle A_1C_1D_1$ üçün $\angle A=\angle A_1$ . $\angle ACB=\angle A_1C_1B_1$ olduğu üçün bu bucaqların yarı bölünməsindən alınan bucaqlar da bərabər olacaq ($\angle ACD = \angle A_1C_1D_1$). Deməli oxşarlığın birinci əlamətinə görə $\triangle ACD \sim \triangle A_1C_1D_1$. Bu isə o deməkdir ki,

$ \dfrac{CD}{C_1D_1} = \dfrac{AC}{A_1C_1} = k$

Eynilə hündürlük çəkilərkən alının düzbucaqlı üçbucaqlar da birinci əlamətə görə oxşar olacaq və bu oxşarlıq bizə hündürlüklərin nisbətinin $\dfrac{AC}{A_1C_1}$-ə, yəni $k$-ya bərabər olduğunu verəcək.

Median çəkilərkən isə bu üçbucaqların oturacaqlarının nisbəti bu oturacaqların yarılarının nisbətinə bərabər olduğu üçün alınan üçbucaqlar ikinci əlamətə görə oxşar olacaq. Bu oxşarlıqda da $\triangle ABC$ və $\triangle A_1B_1C_1$-in uyğun olaraq $AC$ və $A_1C_1$ tərəfləri iştirak etdiyindən oxşarlıq əmsalı həmişə $k$-ya bərabər olacaq.

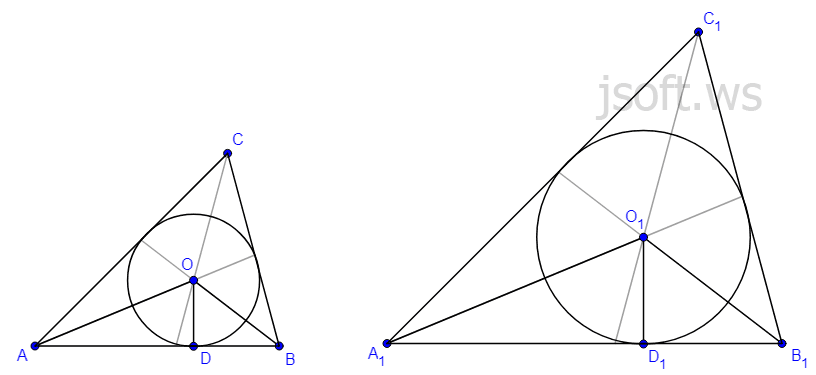
İndi daxilə çəkilmiş çevrələrin radiuslarının mütənasibliyini isbat edək. Bilirik ki, üçbucaq daxilinə çəkilmiş çevrənin mərkəzi onun tənbölənlərinin kəsişmə nöqtəsidir. Deməli, şəkildəki $AOB$ və $A_1O_1B_1$ üçbucaqları birinci əlamətə görə oxşardır. Çünki $\angle OAB = \angle O_1A_1B_1$ və $\angle OBA = \angle O_1B_1A_1$. $OD$ və $O_1D_1$ isə uyğun olaraq $\triangle AOB$ və $\triangle A_1O_1B_1$-in hündürlükləri olduğu üçün yuxarıda isbat etdiyimizə görə

$\dfrac{OD}{O_1D_1}= \dfrac{AB}{A_1B_1} = k$

Bu hündürlüklər isə daxilə çəkilmiş çevrələrin radiuslarıdır.

Xaricə çəkilmiş çevrələrin radiuslarının mütənasibliyini isbat etmək üçün üçbucağın sahəsini onun xaricinə çəkilmiş çevrə radiusu ilə ifadə edən düstura müraciət etsək:

$R=\dfrac{AB \cdot BC \cdot AC}{4S} \\[25pt] R_1 = \dfrac{A_1B_1 \cdot B_1C_1 \cdot A_1C_1}{4S_1}$

Oxşar üçbucaqlar üçün $\dfrac{S}{S_1} = k^2$ olduğundan $S = k^2 \cdot S_1$. $AB$, $BC$ və $AC$ tərəflərini də ikinci xassənin isbatında olduğu kimi uyğun olaraq $A_1B_1$, $B_1C_1$ və $A_1C_1$ ilə ifadə etsək aşağıdakı bərabərliyi alarıq.

$\dfrac{R}{R_1}=\dfrac{\dfrac{AB \cdot BC \cdot AC}{4 \cdot S} }{\dfrac{A_1B_1 \cdot B_1C_1 \cdot A_1C_1}{4 \cdot S_1} } = \\[30pt]
= \dfrac{\dfrac{k^3 \cdot A_1B_1 \cdot B_1C_1 \cdot A_1C_1}{4 k^2 \cdot S_1} } {\dfrac{A_1B_1 \cdot B_1C_1 \cdot A_1C_1}{4 \cdot S_1} } = k$

Əgər üçbucaqların xətti elementlərini $l$ ilə işarə etsək sonuncu xassəni ümumi şəkildə belə ifadə etmək olar.

$\dfrac {l_{ABC}}{l_{A_1B_1C_1}} = k$

Məsələ

Əvvəlcə özünüz həll etməyə çalışın

Digər məqalələr