Yaranma tarixi:
Çevrənin və düz xəttin tənliyi
tənlik
Əgər müstəvidə verilmiş fiqurun istənilən nöqtəsinin $(x; y)$ koordinatları verilmiş tənliyi ödəyirsə bu tənliyə həmin fiqurun tənliyi deyilir. Bu tərifi tərsinə də demək olar. Əgər verilmiş tənliyi ödəyən istənilən ədədlər cütlüyü verilmiş fiqurun üzərindədirsə, bu tənlik həmin fiqurun tənliyidir.
Çevrənin tənliyi
Mərkəzi $O(a; b)$ nöqtəsində olan $R$ radiuslu çevrənin tənliyini verək. Çevrə üzərində ixtiyari A(x; y) götürsək, bu nöqtədən $O$ mərkəzinə qədər məsafə $R$ olmalıdır. Nöqtələr arasındakı məsafə düsturuna görə
$R^2 = (x-a)^2+(y-b)^2$
Beləliklə, biz çevrənin tənliyini aldıq.

Şəkil 1
Düz xəttin tənliyi
Dekart koordinat sistemində ixtiyarı düz xətt aşağıdakı tənliklə verilir.
$ax+by+c=0$
$a$, $b$, $c$ istənilən ədədlərdir. $a$ və $b$ ədədlərindən heç olmazsa biri sıfırdan fərqlidir. Bunu isbat edək.

Şəkil 2
Tutaq ki, hər hansı $h$ xətti verilib (Şəkil 2). Bu düz xəttə perpendikulyar olan xətt çəkək və bu xətt üzərində iki $A_1$ və $A_2$ nöqtələrini qeyd edək. $A_1(x_1; y_1) $və $A_2(x_2; y_2)$ olsun. Parçanın ortasından qaldırılan perpendikulyar barədə teoremə görə $h$ üzərindəki ixtiyari $A(x; y)$ nöqtəsi $A_1$ və $A_2$ nöqtələrindən eyni məsafədədir. Ona görə nöqtələrin koordinatları aşağıdakı tənliyi ödəyir.
$(x-x_1)^2+(y-y_1)^2=(x-x_2)^2+(y-y_2)^2 \Rightarrow \\
x^2-2x_1x+x_1^2+y^2-2y_1y+y_1^2 = x^2-2x_2x+x_2^2+y^2-2y_2y+y_2^2 \Rightarrow \\
2(x_2-x_1)x+2(y_2-y_1)y+(x_1^2+y_1^2-x_2^2-y_2^2)=0$
Aşağıdakı işarələməni aparaq:
$2(x_2-x_1)=a$, $2(y_2-y_1)=b$, $x_1^2+y_1^2-x_2^2-y_2^2=c$
Onda tənliyimiz sadə şəklə düşəcək:
$ax+by+c=0$
İşarələmədən görünür ki, $a$ və $b$ eyni zamanda sıfır olsa $x_2=x_1$ və $y_2=y_1$ olacaq, yəni $A_1$ və $A_2$ nöqtələri üst-üstə düşəcək.



Şəkil 3
Əgər $a=0$, $b \ne o$ olarsa, tənlik $by+c=0 \Rightarrow y= - \dfrac{c}{b}$. Yəni $x$ qiymətindən asılı olmayaraq $y$ sabit ədədə bərabərdir. Deməli düz xətt absis oxuna paralel olub ordinat oxunu $- \dfrac{c}{b}$ nöqtəsində kəsir.
Eynilə $b=0$, $a \ne 0$ olarsa düz xətt ordinat oxuna paralel olub absis oxunu $-\dfrac{c}{a}$ nöqtəsində kəsəcək.
$c=0$ olarsa, $(0; 0)$ nöqtəsi düz xəttin tənliyini ödəyir. Yəni düz xətt koordinat başlanğıcından keçir. Hər üç hal Şəkil 3-də göstərilib.
Düz xəttin bucaq əmsalı
Əgər düz xətin tənliyində $y$ əmsalı sıfırdan fərqlidirsə bu tənliyi $y$-ə görə həll etmək olar.
$ax+by+c=0 \Rightarrow y= - \dfrac{a}{b}x - \dfrac{c}{b}$
Burada $-\dfrac{a}{b}=k$, $-\dfrac{c}{b}=l$ işarələsək $y=kx+b$ alarıq.
$k$ əmsalının həndəsi olaraq nə demək olduğunu aydınlaşdıraq. Düz xətt üzərində iki nöqtə götürək. $A(x_1; y_1)$ və $B(x_2; y_2)$ nöqtələrinin koordinatları düz xəttin tənliyini ödəyir.
$y_1=kx_1+l$, $y_2=kx_2+l$
Bu tənlikləri bir-birindən çıxaq
$y_2-y_1=k(x_2-x_1) \Rightarrow k=\dfrac{y_2-y_1}{x_2-x_1}$
Şəkil 4-ə baxsaq tangensin tərifinə görə, $\dfrac{y_2-y_1}{x_2-x_1}=tg \alpha$, Şəkil 5-də isə $\dfrac{y_2-y_1}{x_2-x_1} = -tg \alpha $ olduğunu görərik.
Deməli, $k$ əmsalı işarə dəqiqliyi ilə bu xəttin $x$ oxu ilə əmələ gətirdiyi bucağın tangensinə bərabərdir. Ona görə də düz xəttin tənliyində $k$-ya bucaq əmsalı deyilir.

Şəkil 4

Şəkil 5
Buradan aydın oldu ki, iki düz xətt bir-birinə paralel olarsa onların hər ikisi eyni bucaq əmsalına malik olmalıdır.
$y=k_1x+l_1$ və $y=k_2x+l_2$ düz xətlərinin paralel olması üçün $k_1=k_2$ olmalıdır.
Bu düz xətlər perpendikulyar olarsa onlar arasındakı bucaq $90°$ olmalıdır. Yəni birinin absis oxu ilə əmələ gətiridyi bucaq $\alpha$ olarsa, o birinin bucağı $\alpha + 90°$ olmalıdır. Yuxarıda isə göstərdik ki bucaq əmsalı həmin $\alpha$ bucağının tangensidir. Deməli,$k_1=tg \alpha$ olarsa
$k_2=tg (90°+\alpha) = \dfrac{sin (90°+\alpha) }{cos(90°+\alpha) } = \\[15pt] =\dfrac {sin 90° cos \alpha + cos 90° sin\alpha }{cos 90° cos \alpha - sin 90° sin \alpha } = \dfrac {cos \alpha}{-sin \alpha} = -ctg \alpha = -\dfrac {1}{k_1}$
Biz aldıq ki, iki düz xətt perpendikulyar olarsa onların bucaq əmsallarının hasili $-1$ olmalıdır ($k_1 k_2 =-1$).
Digər məqalələr

Çevrə və bucaqların 6 xassəsi
Kəsişən vətərlər arasındakı bucaq həmin bucağın tərəfləri arasında qalan qövslərin ölçüləri cəminin yarısına bərabərdir. Çevrəni kəsən iki düz xətt arasındakı bucaq, həmin bucağın kəsişmədə əmələ gətirdiyi böyük qövs ilə kiçik qövsün fərqinin yarısına bərabərdir.

Kəpənək teoremi
Tutaq ki, M nöqtəsi çevrənin PQ vətərinin orta nöqtəsidir. Həmin M nöqtəsindən iki AB və CD vətərləri çəkək. AD parçasının PQ vətərini kəsən nöqtəni X, BC parçasının PQ vətərini kəsən nöqtəni Y ilə işarə edək. Onda M nöqtəsi XY parçasının da orta nöqtəsi olacaq.
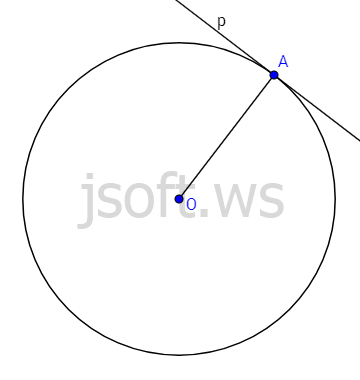
Çevrəyə toxunan
Əgər çevrə və düz xəttin yalnız bir orta nöqtəsi varsa bu düz xəttə çevrəyə toxunan deyilir.Çevrəyə toxunan, toxunma nöqtəsindən çəkilmiş radiusa perpendikulyardır.

Çevrə və Dairə
Müstəvidə verilmiş nöqtədən eyni məsafədə olan nöqtələrin əmələ gətirdiyi həndəsi fiqura çevrə deyilir. Müstəvinin çevrə ilə məhdudlaşmış hissəsinə dairə edilir.
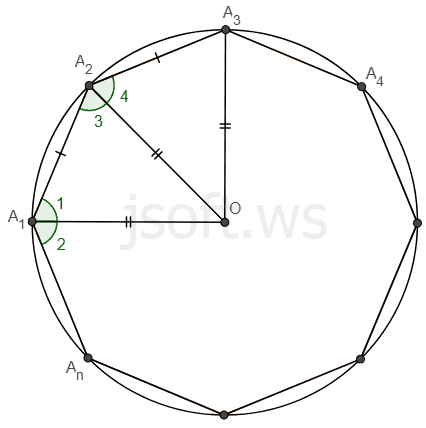
Düzgün çoxbucaqlının xaricinə və daxilinə çəkilmiş çevrələr
Əgər çoxbucaqlının bütün təpələri çevrə üzərindədirsə, bu çevrəyə çoxbucaqlının xaricinə çəkilmiş çevrə deyilir. Əgər çoxbucaqlının bütün tərəfləri çevrəyə toxunursa, bu çevrəyə çoxbucaqlı daxilinə çəkilmiş çevrə deyilir. İstənilən düzgün çoxbucaqlının xaricinə və daxilinə həmişə çevrə çəkmək olar.

Çevrə uzunluğu və dairənin sahəsi
Çevrə uzunluğunu və dairənin sahəsini tapmaq üçün onun daxilinə və xaricinə düzgün 6-bucaqlı çəkək. Daxilə çəkilmiş 6-bucaqlının perimetri p, sahəsi isə s, xaricə çəkilmiş 6-bucaqlını perimetri P, sahəsi isə S olsun.

Çevrə vətərinin 9 xassəsi
Çevrənin mərkəzindən eyni məsafədə olan vətərlər bərabərdir. Əgər vətərlər bərabər mərkəzi bucaqlar qarşısındadırsa onlar bərabərdir. Əgər diametr vətərə perpendikulyardırsa onun mərkəzindən keçir. Eyni vətərə eyni tərəfdən söykənən daxili bucaqlar bərabər, müxtəlif tərəflərdən söykənən bucaqların cəmi 180°-yə bərabərdir.

Daxilə çəkilmiş və mərkəzi bucaqlar
Təpəsi çevrənin mərkəzində olan bucağa mərkəzi bucaq deyilir. Təpəsi çevrə üzərində olub tərəfləri çevrənin tərəflərini kəsən bucağa daxili bucaq deyilir. Daxili bucaq söykəndiyi qövsün yarısı ilə ölçülür.

Müstəvidə dekart koordinat sistemi
Bu koordinat sistemində ixtiyari A nöqtəsini 2 kordinat ilə təsvir etmək olar. Nöqtənin koordinatları birinci absis olmaqla A(x; y) kimi göstərilir.
© Müəllif hüquqları qorunur
Bu saytdakı bütün məqalələr Cəfər N.Əliyev tərəfindən yazılıb. Onlar hər hansı üçüncu şəxs tərəfindən digər resurslarda çap edilərsə mənbə və müəllifin adı göstərilməlidir. Sayt özü həmin şərtlərə əməl edir.
