Yaranma tarixi: 28 Noyabr, 2017

Çevrəyə toxunan

Əgər çevrə və düz xəttin yalnız bir ortaq nöqtəsi varsa bu düz xəttə çevrəyə toxunan deyilir.

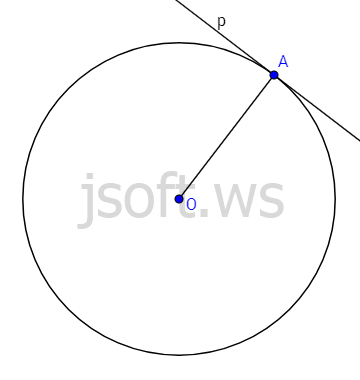
Teorem: Çevrəyə toxunan, toxunma nöqtəsindən çəkilmiş radiusa perpendikulyardır.

İsbatı: Tutaq ki, $p$ xətti mərkəzi $O$ nöqtəsində olan çevrəyə $A$ nöqtəsindən çəkilmiş toxunandır. İsbat etməliyik ki, $p$ düz xətti $OA$ radiusuna perpendikulyardır.

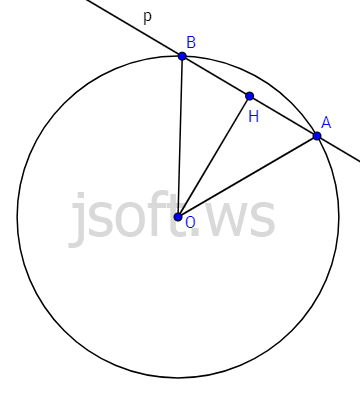
Tutaq ki, bu belə deyil. Onda $OA$ radiusu $p$ düz xəttinə çəkilmiş mail olacaq. Yəni $O$ nöqtəsindən $p$ düz xəttinə perpendikulyar endirsək bu perpendikulyarın uzunluğu radiusdan kiçik olacaq, çünki nöqtədən düz xəttə perpendikulyar və mail çəksək, mail həmişə perpendikulyardan böyükdür.

Bu perpendikulyarın düz xətt ilə kəsişmə nöqtəsini $H$ ilə işarə edək və həmin $H$ nöqtəsindən əks tərəfə $AH$ uzunluqda parça ayıraq. Bu parçanın ucunu $B$ ilə işarələsək, $AH=BH$. $OH$ perpendikulyarı $AB$ parçasının ortasında qaldığına görə əvvəl isbat etdiyimiz teoremə əsasən bu perpendikulyar $A$ və $B$ nöqtələrindən eyni məsafədə olan nöqtələrin həndəsi yeridir, yəni $OB=OA=r$. Deməli, $B$ nöqtəsi də çevrənin üzərindədir. Bu isə şərtə ziddir. Çünki şərtə görə toxunan ilə çevrənin yalnız bir ortaq nöqtəsi ola bilər.

Deməli $p$ düz xətti $OA$ radiusuna perpendikulyardır. Teorem isbat olundu.

Çevrə xaricində olan nöqtədən bu çevrəyə iki toxunan çəkək. Şəklə baxsaq, $AB$ və $AC$ parçaların $A$ nöqtəsindən çəkilmiş toxunan parçalar adlanır.

Teorem: Çevrə xaricindəki nöqtədən çəkilmiş toxunan parçalar bərabərdir və bu nöqtədən çevrənin mərkəzinə çəkilmiş düz xətt ilə bərabər bucaqlar əmələ gətirir.

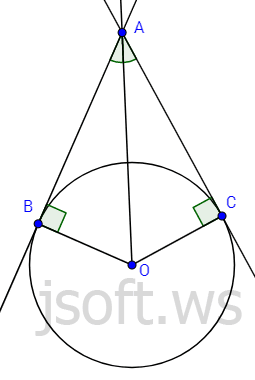
İsbatı: Toxunanın tərifinə görə $\angle OBA = \angle OCA = 90°$. $OA$ tərəfi isə ortaqdır. $OB=OC$, çünki hər ikisi radiusdur. Onda $\triangle OAB = \triangle OAC$, çünki bu iki düzbucaqlı üçbucağın katet və hipotenuzları bərabərdir. Deməli, $AB=AC$ və $\angle OAB = \angle OAC$.

Teorem: Radiusun çevrə üzərində olan sonundan keçib ona perpendikulyar olan düz xətt, bu çevrənin toxunanıdır.

İsbatı: Biz isbat etməliyik ki, həmin düz xətt ilə çevrənin yeganə toxunma nöqtəsi var. Düz xətt radiusun çevrə üzərindəki sonundan keçdiyi üçün bu düz xətt ilə çevrənin toxunma nöqtəsi artıq var. İsbat etməliyik ki, bu nöqtə yeganədir. Tutaq ki, həmin düz xətt çevrəni başqa bir nöqtədə də kəsir. Onda həmin nöqtəni çevrənin mərkəzi ilə birləşdirsək çevrənin mərkəzindən eyni xəttə uzunluğu radiusa bərabər olan iki xətt çəkmiş oluruq. Bunlardan biri həmin xəttə perpendikulyar.

Biz isə bilirik ki, düz xətt xaricindəki nöqtədən bu düz xəttə yeganə perpendikulyar endirmək olar. Deməli ikinci xətt maildir. Digər teoremə görə düz xətt xaricindəki nöqtədən bu düz xəttə perpendikulyar və mail çəksək mail həmişə perpendikulyardan uzun olacaq. Biz isə bilirik ki, bu parçaların hər ikisinin uzunluğu radiusa bərabərdir. Burada ziddiyyətə gəldik. Yəni düz xətt çevrəni ikinci bir nöqtədə kəsə bilməz. Yəni bu düz xətt toxunandır.

Digər məqalələr

Çevrə və bucaqların 6 xassəsi

Kəsişən vətərlər arasındakı bucaq həmin bucağın tərəfləri arasında qalan qövslərin ölçüləri cəminin yarısına bərabərdir. Çevrəni kəsən iki düz xətt arasındakı bucaq, həmin bucağın kəsişmədə əmələ gətirdiyi böyük qövs ilə kiçik qövsün fərqinin yarısına bərabərdir.

Kəpənək teoremi

Tutaq ki, M nöqtəsi çevrənin PQ vətərinin orta nöqtəsidir. Həmin M nöqtəsindən iki AB və CD vətərləri çəkək. AD parçasının PQ vətərini kəsən nöqtəni X, BC parçasının PQ vətərini kəsən nöqtəni Y ilə işarə edək. Onda M nöqtəsi XY parçasının da orta nöqtəsi olacaq.

Çevrə və Dairə

Müstəvidə verilmiş nöqtədən eyni məsafədə olan nöqtələrin əmələ gətirdiyi həndəsi fiqura çevrə deyilir. Müstəvinin çevrə ilə məhdudlaşmış hissəsinə dairə edilir.

Çevrənin və düz xəttin tənliyi

Əgər müstəvidə verilmiş fiqurun istənilən nöqtəsinin (x; y) koordinatları verilmiş tənliyi ödəyirsə bu tənliyə həmin fiqurun tənliyi deyilir. Düz xəttin tənliyi ax+by+c=0 kimidir.

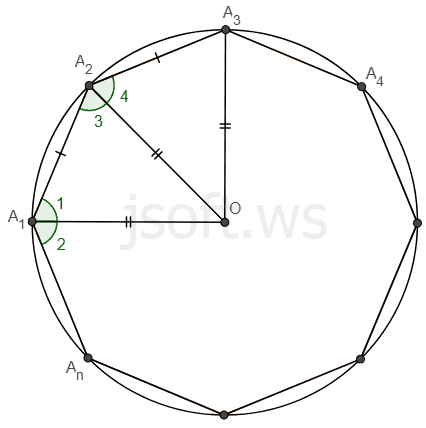
Düzgün çoxbucaqlının xaricinə və daxilinə çəkilmiş çevrələr

Əgər çoxbucaqlının bütün təpələri çevrə üzərindədirsə, bu çevrəyə çoxbucaqlının xaricinə çəkilmiş çevrə deyilir. Əgər çoxbucaqlının bütün tərəfləri çevrəyə toxunursa, bu çevrəyə çoxbucaqlı daxilinə çəkilmiş çevrə deyilir. İstənilən düzgün çoxbucaqlının xaricinə və daxilinə həmişə çevrə çəkmək olar.

Çevrə uzunluğu və dairənin sahəsi

Çevrə uzunluğunu və dairənin sahəsini tapmaq üçün onun daxilinə və xaricinə düzgün 6-bucaqlı çəkək. Daxilə çəkilmiş 6-bucaqlının perimetri p, sahəsi isə s, xaricə çəkilmiş 6-bucaqlını perimetri P, sahəsi isə S olsun.

Çevrə vətərinin 9 xassəsi

Çevrənin mərkəzindən eyni məsafədə olan vətərlər bərabərdir. Əgər vətərlər bərabər mərkəzi bucaqlar qarşısındadırsa onlar bərabərdir. Əgər diametr vətərə perpendikulyardırsa onun mərkəzindən keçir. Eyni vətərə eyni tərəfdən söykənən daxili bucaqlar bərabər, müxtəlif tərəflərdən söykənən bucaqların cəmi 180°-yə bərabərdir.

Daxilə çəkilmiş və mərkəzi bucaqlar

Təpəsi çevrənin mərkəzində olan bucağa mərkəzi bucaq deyilir. Təpəsi çevrə üzərində olub tərəfləri çevrənin tərəflərini kəsən bucağa daxili bucaq deyilir. Daxili bucaq söykəndiyi qövsün yarısı ilə ölçülür.