Ana səhifə :: Riyaziyyat :: Həndəsə :: Oxşarlıq
Yaranma tarixi:
Oxşar fiqurlar
hərəkət oxşarlıq
Əgər iki fiqur bir-birindən oxşarlıq çevrilməsi ilə alınarsa, onlara oxşar fiqurlar deyilir. Fiqurların oxşarlığı $\sim$ ilə işarə edilir. $F \sim F’$ yazılışı belə oxunur: $F$ və $F’$ fiqurları oxşardır.

Teorem: Əgər $F_1$ fiquru $F_2$ fiquruna, $F_2$ fiquru isə $F_3$ fiquruna oxşardırsa, ona $F_1$ fiquru da $F_3$ fiquruna oxşardır.
İsbatı: $F_1$ fiqurunun üzərində iki $X_1$ və $Y_1$ nöqtələrini götürək. Oxşarlıq çevrilməsi $F_1$ fiqurunu $F_2$ fiquruna çevirirsə $X_1$ və $Y_1$ nöqtələrini uyğun olaraq $X_2$ və $Y_2$ nöqtələrinə çevirəcək. Onda
$X_2Y_2 = k_1 \cdot X_1Y_1$
Eynilə $F_2$ fiqurunu $F_3$ fiquruna çevirən oxşarlıq çevrilməsi bu fiqurun $X_2$ və $Y_2$ nöqtələrini uyğun olaraq $X_3$ və $Y_3$ nöqtələrinə çevirəcək. Onda
$X_3Y_3 = k_2 \cdot X_2Y_2 = k_1 \cdot k_2 \cdot X_1Y_1$
Bu isə əmsalı $k_1k_2$ olan yeni oxşarlıq çevrilməsidir ki, $F_1$ fiqurunu $F_3$ fiquruna çevirir.
Oxşarlıq çevrilməsinin xassələrini oxşar fiqurlara tətbiq etsək belə bir nəticə əldə etmiş olarıq.
Nəticə: Oxşar fiqurların uyğun bucaqları bərabər, uyğun tərəfləri mütənasibdir. Mütənasiblik əmsalı isə oxşarlıq əmsalıdır.
Digər məqalələr
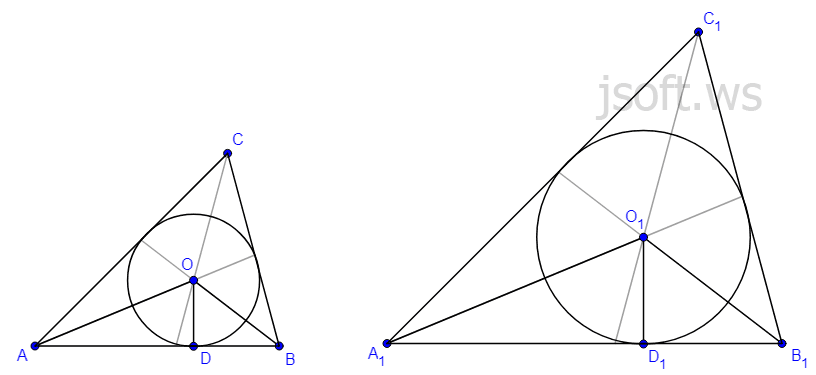
Oxşar üçbucaqların xassələri
Oxşar üçbucaqların perimetrlərinin nisbəti onların oxşarlıq əmsalına bərabərdir. Oxşar üçbucaqlarının xətti elementlərinin nisbəti üçbucaqların oxşarlıq əmsalına bərabərdir.
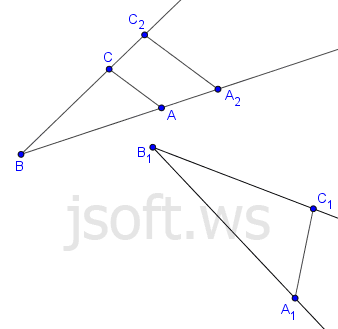
Oxşarlıq çevrilməsinin xassələri
Əgər A, B, C nöqtələri bir düz xətt üzərindədirsə, oxşarlıq çevrilməsi zamanı alınan A', B', C' nöqtələri də bir düz xətt üzərində olacaq. B nöqtəsi A və C arasındadırsa, B' də A' və C' arasında olacaq. Oxşarlıq çevrilməsi zamanı düz xətt düz xəttə, şüa şüaya, parça isə parçaya keçir.

Hərəkət nədir?
Hərəkət, elə çevirmə əməliyyatıdır ki, bunun nəticəsində məsafə saxlanılır. Başqa cür desək, hərəkət müstəvini özünə elə inikas edir ki, onun nəticəsində məsafə dəyişmir.

Oxşarlıq çevrilməsi
F fiqurunun F’ fiquruna çevrilməsi zamanı nöqtələr arasındakı məsafə eyni nisbətdə dəyişərsə bu çevrilmə oxşarlıq çevrilməsi adlanır. Homotetiya oxşarlıq çevrilməsidir.
© Müəllif hüquqları qorunur
Bu saytdakı bütün məqalələr Cəfər N.Əliyev tərəfindən yazılıb. Onlar hər hansı üçüncu şəxs tərəfindən digər resurslarda çap edilərsə mənbə və müəllifin adı göstərilməlidir. Sayt özü həmin şərtlərə əməl edir.
