Yaranma tarixi: 29 Dekabr, 2017

Nöqtə, düz xətt və müstəvi

düz xətt

 

Həndəsənin əsas fiqurları nöqtə, düz xətt və müstəvidir.

Nöqtə

Nöqtə – heç bir ölçüsü olmayan fiqurdur. Ona görə deyirlər ki, nöqtə özündə 0-ölçülü fəzanı əks etdirir. Yəni özü 0-ölçülü fəza olmaqla yanaşı, həm də bu fəzanın yeganə elementidir.

Evklid 300 il bizim eradan əvvəl özünün “Başlanğıc” əsərində nöqtənin tərifini belə verir: “Nöqtə heç bir hissəsi olmayan şeydir”. Hərfi mənada tərcümə isə belədir: “Nöqtə elə bir şeydir ki, onun hissəsi heç nədir”. Nöqtələri böyük latın hərfləri ilə işarə edirlər: $A$, $B$, $C$, ...

Nöqtəyə digər elm sahələrində də rast gəlinir. Onunla adətən bölünməyən hissəciyi işarə edirlər. Belə ki, kimyada atoma, kvant fizikasında isə elementar hissəciklərə nöqtə kimi baxılır. Ümumiyyətlə belə bir fikir mövcuddur ki, bütün kainat sinqulyarlıq nöqtəsindən Böyük partlayış nəticəsində yaranıb.

Sanıram nöqtənin nə olduğunu yetərincə anlada bildim. İndi keçək düz xəttə.

Düz xətt

Düz xəttin yalnız uzunluğu var, eni və qalınlığı isə yoxdur. Düz xətt hər iki tərəfə sonsuz uzanır.

Evklid düz xəttin tərifini belə verir: “Xətt – eni olmayan uzunluqdur. Xəttin ucları nöqtələrdir” Əgər düz xətt hər iki tərəfə sonsuz uzanırsa, onun ucları, yəni nöqtələr sonsuzluqdadır. Digər tərəfdən düz xəttə ardıcıl düzülmüş nöqtələr kimi də baxmaq olar. Deməli nöqtə düz xəttin hər yerində mövcuddur. Bir sonsuzluqdan digər sonsuzluğa qədər uzanan nöqtələr toplusudur düz xətt.

Düz xətti təsəvvür etmək üçün gərilmiş simi gözünüz önünə gətirin. Bu sim düz xəttin bir hissəsidir.

Düz xətti latın əlifbasının kiçik hərfləri ilə işarə edirlər: $a$, $b$, $c$, ... Həmçinin düz xətti onun üzərində olan iki nöqtə ilə də işarə edirlər. Əgər $A$ və $B$ nöqtələri düz xətt üzərində yerləşirsə bu düz xətti $AB$ düz xətti kimi də adlandırırlar.

Süa

Düz xətt üzərində olan nöqtə bu düz xətti iki hissəyə bölür. Bu hissələrin hər birinə başlanğıcı həmin nöqtədə olan süa və ya yarım düz xətt deyilir. Başqa cür desək, düz xətt üzərində olan  nöqtə və bu nöqtədən eyni tərəfdə olan nöqtələr toplusundan ibarət fiqura süa deyilir.

Şəkildə $O$ nöqtəsi $a$ xəttini iki şüaya ayırır. Şüanı da ya kiçik latın hərfləri ilə, ya da üzərindəki iki nöqtə ilə işarə edirlər. Bu şərtlə ki, həmin nöqtələrdən biri şüanın başlanğıc nöqtəsi olsun. Məsələn, $OC$ şüası.

Bir düz xətt üzərində olub ümumi başlanğıcları olan iki müxtəlif şüaya əks şüalar və ya tamamlayıcı şüalar deyilir. Şəkildəki $OD$ və $OC$ şüaları tamamlayıcı şüalardır.

Parça

Düz xəttin iki nöqtə ilə məhdudlaşmış hissəsinə parça deyilir. Bu iki nöqtəyə parçanın sonları, arada qalan nöqtələrə isə daxili nöqtələri deyilir.

İki parçanı müqayisə etmək üçün onları bir-birinin üzərinə qoyurlar.  Bir-birinin üzərinə qoyularkən parçalar tamamilə üst-üstə düşərsə bu parçalar bərabər parçalar adlanır.

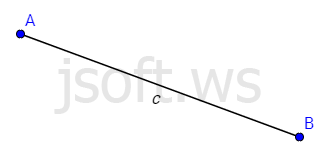
Parçaları ya uç nöqtələri ilə ($AB$ və ya $BA$ kimi), ya da ki, kiçik latın hərfləri ilə işarə edirlər: $a$, $b$, $c$, ...

Müstəvi

Yuxarıdakı mülahizələrdən yəqin ki, özünüz müstəvinin tərifini verə bilərsiniz. Müstəvi – qalınlığı olmayan, ideal düz hamar və bütün tərəflərə sonsuz uzanan fiqurdur.

Evklidə görə “Müstəvi – yalnız eni və uzunluğu olan fiqurdur. Müstəvinin kənarları düz xətlərdər”.

Müstəvini təsəvvür etmək üçün pəncərə şüşəsini və ya stolun səthini yada salın. Müstəviləri kiçik yunan hərfləri ilə işarə edirlər: $\alpha$, $\beta$, $\gamma$, ...

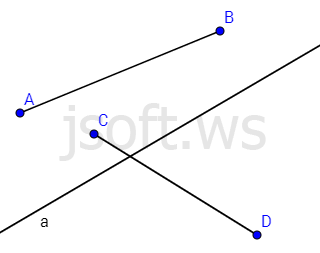
Müstəvi üzərində olan düz xətt onu iki hissəyə bölür ki, hər bir hissə yarımmüstəvi adlanır. Şəkildə $A$ və $B$ nöqtələri eyni yarımmüstəvidə yerləşdiyi üçün $AB$ parçası bu düz xətti kəsmir. $C$ və $D$ nöqtələri isə müxtəlif yarımmüstəvilərdədir, ona görə $CD$ parçası həmin düz xətti kəsir.

Bu məqalə rus dilində

Digər məqalələr