Yaranma tarixi: 10 İyul, 2017

Üçbucaq

Üç təpəsi və üç tərəfi olan qapalı həndəsi fiqura üçbucaq deyilir.

Təpələri $A$, $B$ və $C$ olan üçbucağı $\triangle ABC$ ilə işarə edirlər. Həmçinin $\triangle BCA$, $\triangle CAB$, $\triangle CBA$, və s. kimi işarələmələr də doğrudur. Şəkildəki üçbucağın tərəfləri $AB$, $AC$ və $BC$-dir. Bu üçbucağın təpə bucaqlarını $\angle A$, $\angle B$ və $\angle C$ ilə işarə edirlər.

$AB$ tərəfinin uzunluğunu $|AB|$ kimi işarə edirlər. Söhbət uzunluqdan getdiyi məlum olduğu halda sadəcə olaraq $AB$ kimi işarələmə də mümkündür. Üçbucağın bütün tərəflərinin uzunluqları cəminə onun perimetri deyilir və $P_{ABC}$ kimi işarə edilir.
$$P_{ABC} = |AB|+|AC|+|BC|$$
Bütün tərəfləri və bucaqları uyğun olaraq bir-birinə bərabər olan üçbucaqlar bərabər üçbucaqlar adlanır. Yəni bu üçbucaqları sürüşdürüb üst-üstə salsaq, biri o biri üçbucağı tamamilə örtəcək.

Median. Üçbucağın təpəsini qarşı tərəfin ortası ilə birləşdirən düz xətt parçasına median deyilir.

Hündürlük. Üçbucağın təpəsindən qarşı tərəfin yerləşdiyi xəttə çəkilən perpendikulyara onun hündürlüyü deyilir.

Tənbölən. Üçbucağın təpə bucağını yarı bölüb, bu təpəni qarşı tərəf üzərindəki nöqtə ilə birləşdirən parçaya hündürlük deyilir.

İstənilən üçbucağın üç təpə və üç tərəfi olduğu üçün üç medianı, üç tənböləni və üç hündürlüyü vardır.

Bərabəryanlı üçbucaq

İki tərəfi bərabər olan üçbucağa bərabəryanlı üçbucaq deyilir. Bu bərabər tərəflərə bərabəryanlı üçbucağın yan tərəfləri, üçüncü tərəfə isə oturacağı deyilir.

Bütün tərəfləri bərabər olan üçbucağa bərabərtərəfli üçbucaq deyilir. Bərabərtərəfli üçbucağa düzgün üçbucaq da deyirlər. İstənilən bərabərtərəfli üçbucaq həm də bərabəryanlıdır.

Teorem: Bərabəryanlı üçbucağın oturacaqdakı bucaqları bərabərdir.

İsbatı: Tutaq ki, $\triangle ABC$-də $AB=AC$. İsbat edək ki, $\angle B=\angle C$. $A$ təpəsindən $AF$ tənböləni çəksək üçbucaqların bərabərliyinin birinci əlamətinə görə $\triangle ABF =\triangle ACF$. Çünki $AB=AC$, $AF$ tərəfi ortaqdır, $\angle BAF=\angle CAF$. Bu bərabərlikdən alınır ki, $\angle B=\angle C$.

Teorem: Bərabəryanlı üçbucağın oturacağına çəkilmiş tənbölən həm median, həm də hündürlükdür.

İsbatı: Yuxarıdakı üçbucağa baxaq. İsbat etməliyik ki, $AF$ tənböləni həm median, həm də hündürlükdür. Əvvəlki teoremdə deyildiyi kimi $\triangle ABF = \triangle ACF$ (I əlamətə görə). Buradan $BF=FC$ alınır. Yəni $F$ nöqtəsi $BC$ tərəfini yarı bölür və $AF$ mediandır. Həmçinin üçbucaqların bərabərliyindən $\angle AFB= \angle AFC$ alınır. Bu bucaqlar isə qonşu bucaqlar olduğundan onların cəmi $180°$-yə bərabərdir. Deməli onların hər biri $90°$-dir. Bu da $AF$ parçasının $A$ təpəsindən $BC$ tərəfinə çəkilmiş hündürlük olması deməkdir.

Digər məqalələr

Üçbucaqların həlli

Üçbucağın həlli dedikdə verilmiş 3 element vasitəsilə onun bütün tərəflərinin və bucaqlarının tapılması nəzərdə tutulur. Bu məsələni üç halda araşdıracağıq.

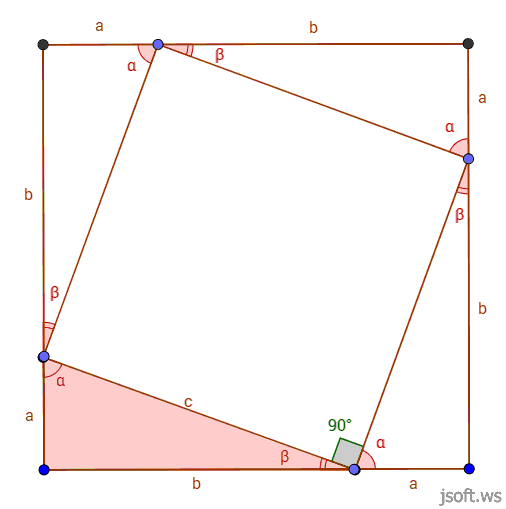
Pifaqor teoremi

Düzbucaqlı üçbucağın katetlərinin kvadratları cəmi hipotenuzun kvadratına bərabərdir. Bu teoremin 370 müxtəlif isbatı mövcuddur. Burada onlardan 5-i verilib.

Oxşar üçbucaqlar

Əgər bir üçbucağın iki bucağı o biri üçbucağın iki bucağına bərabərdirsə bu üçbucaqlar oxşardır. Əgər bir üçbucağın iki tərəfi uyğun olaraq o biri üçbucağın iki tərəfi ilə mütənasib olub, bu tərəflərin əmələ gətirdiyi bucaqlar bərabərdirsə, bu üçbucaqlar oxşardır. Üç tərəfi mütənasib olan üçbucaqlar oxşardir.

Üçbucaqların bərabərlik əlamətləri

İki tərəf və arasındakı buçağı bərabər olan üçbucaqlar bərabərdir. Bir tərəf və ona söykənən bucaqları bərabər olan üçbucaqlar bərabərdir.

Bərabərtərəfli üçbucaq

Bütün tərəfləri bərabər olan üçbucağa bərabərtərəfli üçbucaq deyilir. Bərabərtərəfli üçbucaqda bütün bucaqlar 60°-dir. Belə üçbucaqlarda median, hündürlüyk və tənbölənlər üst-üstə düşür.

Kosinuslar teoremi

Üçbucağın istənilən tərəfinin kvadratı, qalan iki tərəfin kvadratları cəmi ilə onların hasilinin iki mislinin aralarındakı bucağın kosinusuna hasilinin fərqinə bərabərdir.

Sinuslar teoremi

Üçbucağın tərəfləri qarşı bucaqların sinusları ilə mütənasibdir. Bunu isbat etmək üçün isbat etməliyik ki, üçbucağın sahəsi onun ixtiyarı iki tərəfinin uzunluqları hasilinin yarısı ilə bu tərəflər arasında qalan bucağın sinusu hasilinə bərabərdir.

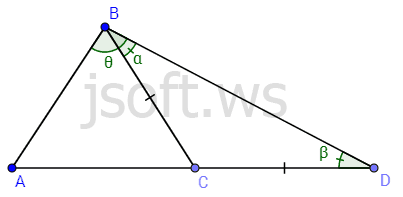
Üçbucaq bərabərsizliyi

Üçbucağın istənilən tərəfi digər iki tərəfin cəmindən kiçikdir. Üçbucağın böyük tərəfi qarşısında böyük bucağı durur. Üçbucağın böyük bucağı qarşısında böyük tərəfi durur.

Median, tənbölən, hündürlük

Üçbucağın medianları bir nöqtədə kəsişib bu kəsişmə nöqtəsində təpədən 2:1 nisbətində bölünür. Üçbucağın tənbölənləri bir nöqtədə kəsişib qarşı tərəfi bitişik tərəflərlə mütənasib hissələrə bölür. Üçbucağın hündürlükləri bir nöqtədə kəsişir.

Fales teoremi

Əgər bucağın tərəflərini kəsən xətlər onun bir tərəfində bərabər parçalar ayırırsa, o biri tərəfində də bərabər parçalar ayırır. Bucağın tərəflərini kəsən paralel xətlər onları mütənasib hissələrə bölür.

Heron düsturu

Bizim Eranın I əsrində yaşamış İskəndəriyyəli Heron həndəsə, mexanika, hidrostatika və optika ilə məşğul olurdu. Onun verdiyi Heron düsturunun köməyi ilə sahəni üç tərəf vasitəsilə tapmaq mümkündür.

Üçbucağın bucaqlarının cəmi

Üçbucağın daxili bucaqlarının cəmi 180°-yə bərabərdir. Üçbucağın xarici bucağı onunla qonşu olmayan iki daxili bucağın cəminə bərabərdir.