Yaranma tarixi: 06 İyul, 2017

tg(a)+tg(b), tg(a)-tg(b), ctg(a)+ctg(b), ctg(a)-ctg(b)

Bu məqalədə $tg \alpha \pm tg \beta$ və $ctg \alpha \pm ctg \beta$ ifadələrinə baxacğıq. Əvvəlcə $tg \alpha + tg \beta$-ya baxaq. Bu ifadəni araşdırdıqdan sonra digər hallar analoji alınacaq.

$tg \alpha + tg \beta = \dfrac {sin \alpha}{cos \alpha} + \dfrac {sin \beta}{cos \beta}$

Çünki əsas triqonometrik bərabərliklərdən bilirik ki, $tg \alpha = \dfrac {sin \alpha}{cos \alpha}$ və $tg \beta = \dfrac {sin \beta}{cos \beta}$. İndi ortaq məxrəc tapaq.

$\dfrac {sin \alpha}{cos \alpha} + \dfrac {sin \beta}{cos \beta} = \dfrac {sin \alpha \cos \beta + cos\alpha \ sin \beta}{cos \alpha \ cos\beta}$

$sin (\alpha+\beta)$ açılışından bilirik ki,

$sin (\alpha+\beta) = sin\alpha \ cos \beta + cos\alpha \ sin \beta$

Onda

$\dfrac {sin \alpha \cos \beta + cos\alpha \ sin \beta}{cos \alpha \ cos\beta} = \dfrac {sin(\alpha + \beta)}{cos\alpha \ cos \beta}$

Deməli,

$tg \alpha + tg \beta = \dfrac {sin(\alpha + \beta)}{cos\alpha \ cos \beta}$

Eynilə,

$tg \alpha - tg \beta = \dfrac {sin \alpha}{cos \alpha} - \dfrac {sin \beta}{cos \beta} = \\[15pt] =\dfrac {sin \alpha \cos \beta - cos\alpha \ sin \beta}{cos \alpha \ cos\beta} = \dfrac {sin(\alpha - \beta)}{cos\alpha \ cos \beta}$

Yuxarıdakı $sin (\alpha - \beta) = sin \alpha \ cos \beta - cos \alpha \ sin \beta$ açılışı da burada göstərilib.

İndi $ctg \alpha + ctg\beta$-ya baxaq.

$ctg \alpha + ctg \beta = \dfrac {cos \alpha}{sin \alpha} + \dfrac {cos \beta}{sin \beta} = \\[15pt] =\dfrac {cos \alpha \ sin\beta + cos\beta \ sin \alpha}{sin \alpha \ sin\beta} = \dfrac {sin(\alpha + \beta)}{sin\alpha \ sin \beta}$

Eynilə,

$ctg \alpha - ctg \beta = \dfrac {cos \alpha}{sin \alpha} - \dfrac {cos \beta}{sin \beta} = \\[15pt] =\dfrac {cos \alpha \ sin\beta - cos\beta \ sin \alpha}{sin \alpha \ sin\beta} = \dfrac {sin(\beta - \alpha)}{sin\alpha \ sin \beta} = -\dfrac {sin(\alpha - \beta)}{sin\alpha \ sin \beta}$

Ümumiləşdirib deyilənləri belə yazmaq olar:

$\mathbf{tg \alpha \pm tg \beta = \dfrac {sin (\alpha \pm \beta)}{cos \alpha \ cos \beta}; \ \ ctg \alpha \pm ctg \beta = \pm \dfrac {sin (\alpha \pm \beta)}{sin \alpha \ sin \beta}}$

Digər məqalələr

İkiqat və üşqat bucağın triqonometrik funksiyaları

$\sin 2x$, $\cos 2x$, $\mbox{tg} 2x$, $\mbox{ctg} 2x$, $\sin 3x$, $\cos 3x$, $\mbox{tg}3x$, $\mbox{ctg}3x$ ikiqat və üçqat bucaqların triqonometrik düsturlarını çıxarmaq üçün cəmin triqonometrik funksiya düsturlarından istifadə edəcəyik.

Triqonometrik funksiyaların çevrilmə qaydaları

Əgər triqonometrik funksiyanın arqumenti özündə $n \dfrac {\pi}{2}$ saxlayırsa, yəni bucaq $n \dfrac {\pi}{2} + \alpha$ və ya $n \dfrac {\pi}{2}-\alpha$ şəklində göstərilibsə onda $n$-in tək və cütlüyündən asılı olaraq iki hal mümkündür. Əgər $n$ tək ədəddirsə, onda $n \dfrac {\pi}{2}$-ni arqumentdən götürüb funksiyanı onun "konfunksiyasına" çevirə bilərik.

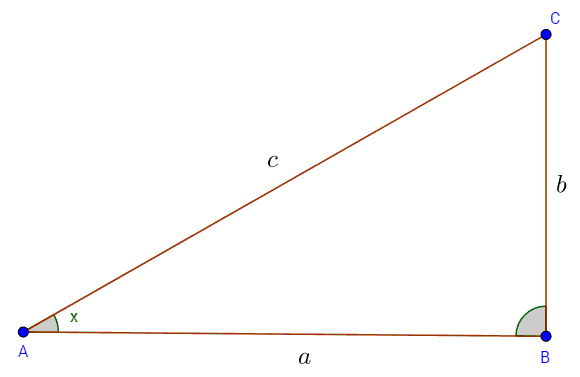
Əsas triqonometrik bərabərliklər

Bu məqalədə əsas triqonometrik bərabərliklər göstərilir və hər biri ayrı-ayrılıqda izah edilir.

sin(a+b), sin(a-b), cos(a+b), cos(a-b)

$\sin(\alpha+\beta)$, $\sin(\alpha-\beta)$, $\cos(\alpha+\beta)$ və $\cos(\alpha-\beta)$ məktəb triqonometriyasından başlayaraq, sonra da institut kursunda ən çox rast gəlinən triqonometrik düsturlardandır.

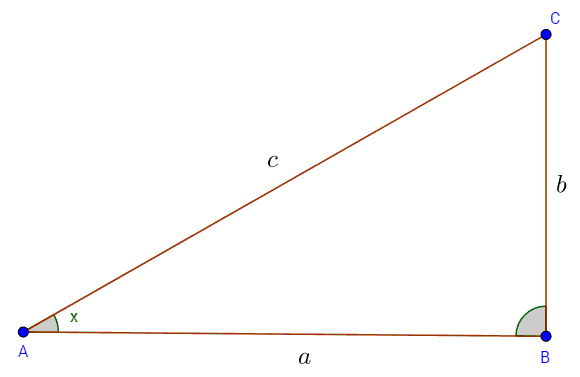
Yarım bucağın triqonometrik funksiyaları

Yarım bucağın triqonometrik düsturları ikiqat bucağın kosinusu üçün olan düsturlara əsaslanır.

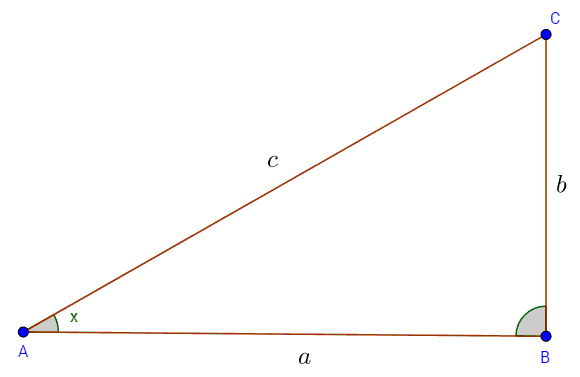
Tangenslərin cəmi və hasili

Əgər $\alpha + \beta+ \gamma = \pi$ olarsa bu bərabərlik doğrudur: $\mbox{tg} \alpha + \mbox{tg} \beta + \mbox{tg} \gamma = \mbox{tg} \alpha \ \mbox{tg} \beta \ \mbox{tg} \gamma$

tg(a+b), tg(a-b), ctg(a+b), ctg(a-b)

$\mbox{tg}(\alpha+\beta)$, $\mbox{tg}(\alpha-\beta)$, $\mbox{ctg}(\alpha+\beta)$ və $\mbox{ctg}(\alpha-\beta)$ ifadələrini açaraq nisbət şəlində göstərək.

sin(a)+sin(b), sin(a)-sin(b), cos(a)+cos(b), cos(a)-cos(b)

$\sin \alpha + \sin \beta$, $\sin \alpha-\sin \beta$, $\cos \alpha+\cos \beta$, $\cos \alpha-cos \beta$ cəm və fərqlərini hasil ilə ifadə edək. Bunun üçün $\alpha$ və $\beta$-ya belə bir əvəzləmə aparaq.