Yaranma tarixi: 20 Mart, 2018

Paraleloqramın sahəsi

Burada paraleloqramın sahəsini tapmaq üçün məlum olan bütün düsturları yığmışıq.

I düstur

Əvvəlcə ən sadə düsturu verək. Paraleloqramın sahəsi onun oturacağı ilə hündürlüyü hasilinə bərabərdir.

$S=ah$

Burada $a$ oturacaq, $h$ bu oturacağa çəkilmiş hündürlükdür. Bu düsturun çıxarılışı artıq verilib.

II düstur

Paraleloqramın sahəsi onun iki tərəfi ilə bu tərəflər arasında qalan bucağın sinusu hasilinə bərabərdir.

$S=ab \ sin \varphi$

$a$ və $b$ tərəflər, $\varphi$ isə onlar arasındakı bucaqdır.

Əgər paraleloqramı diaqonal ilə iki üçbucağa bölsək, bu üçbucaqlar üç tərəfinə görə bərabər olacaq. Ona görə paraleloqramın sahəsi bu üçbucaqlardan birinin sahəsinin iki mislinə bərabər olacaq. Üçbucağın sahəsini $S_{\triangle}$ ilə işarə etsək

$S=2 \cdot S_{\triangle}$

Həmin üçbucağın sahəsini iki tərəf və arasındakı bucaq vasitəsilə tapıb yerinə yazaq.

$S=2 \cdot \dfrac{1}{2} ab \ sin \varphi = ab \ sin \varphi$

III düstur

Paraleloqramın sahəsi onun diaqonalları və bu diaqonallar arasında qalan bucağın sinusu hasilinin yarısına bərabərdir.

$S = \dfrac{1}{2} d_1 d_2 \ sin \varphi$

$d_1$ və $d_2$ diaqonallar, $\varphi$ isə onların kəsişməsindən alınan bucaqdır.

Kəsişmədə 4 bucaq alınır. Bunlar iki-iki qarşılıqlı bucaqlardır. $sin \varphi = sin (\pi - \varphi)$ olduğu üçün hansı bucağı götürməyin fərqi yoxdur. Bu düsturun da çıxarılışı artıq verilib.

Digər məqalələr

Üçbucaq daxilinə çəkilmiş kvadrat

Əgər kvadratın tərəfi üçbucağın bir tərəfində yerləşib digər iki təpəsi üçbucağın digər tərəfləri üzərindədirsə bu kvadrat üçbucaq daxilinə çəkilmiş kvadrat adlanır. Üçbucaq daxilinə çəkilmiş kvadratın tərəfi bu üçbucağın oturacağı ilə hündürlüyü hasilinin, həmin oturacaq ilə həmin hündürlük cəminə nisbətinə bərabərdir.

Düzbucaqlının sahəsi

Düzbucaqlının sahəsi onun tərəflərinin hasilinə bərabərdir. Düzbucaqlının sahəsi onun xaricinə çəkilmiş çevrənin radiusu kvadratının, düzbucaqlının diaqonalları arasındakı bucağın sinusuna hasilinin iki mislinə bərabərdir.

Rombun sahəsi

Romb paraleloqramın xüsusi hali olduğu üçün paraleloqramın sahə düsturları burada da keçərlidir. Rombun sahəsi daxilinə çəkilmiş çevrənin diametrinin onun tərəfinə hasilinə bərabərdir. Bundan başqa bu sahə daxilə çəkilmiş çevrənin diametrinin iki tərəf arasındakı bucağın sinusina nisbətinə bərabərdir.

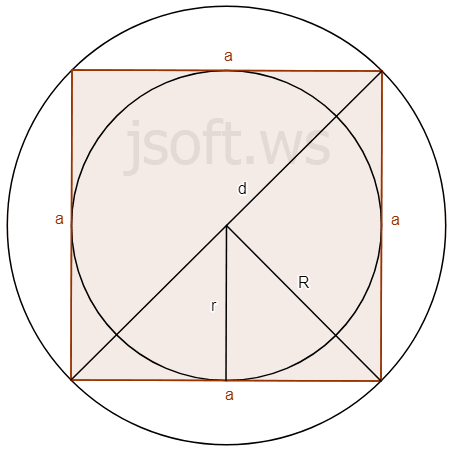
Kvadratın sahəsi

Kvadratın sahəsi daxilinə çəkilmiş çevrənin radiusu kvadratının dörd mislinə bərabərdir. Bu sahə həmçinin onun diaqonalının kvadratının yarısına bərabərdir. Kvadratın sahəsi onun xaricinə çəkilmiş çevrənin radiusu kvadratının iki mislinə bərabərdir.

Trapesiyanın sahəsi

Trapesiyanın sahəsi oturacaqlarının cəmini yarısı ilə hündürlüyü hasilinə bərabərdir. Bu sahəni trapesiyanın diaqonalları ilə bu diaqonalların kəsişməsindən alınan bucağın sinusu hasilinin yarısı kimi də ifadə etmək olar.

Dördbucaqlının sahəsi

Qabarıq dördbucaqlının sahəsi onun diaqonalları ilə bu diaqonalların kəsişmə nöqtəsində əmələ gələn bucağın sinusu hasilinin yarısına bərabərdir. Əgər bu dördbucaqlının xaricinə çevrə çəkmək mümkündürsə onun sahəsini Braxmaqupta düsturu vasitəsi ilə də tapmaq olar.