Yaranma tarixi: 22 Mart, 2018

Papp teoremi

Bu teorem yunan riyaziyyatçısı İskəndəriyyəli Pappın adı ilə bağlıdır. Papp bu teoremi eramızın 4-cü əsrində isbat edib. Haqqında danışılacaq teorem Pifaqor teoreminin analoqudur. Fərqi isə ondadır ki, Papp teoremi üçbucaq üzərinə heç bir məhdudiyyət qoymur.

Papp teoremı: Tutaq ki, ixtiyarı $ABC$ üçbucağı verilib. $ABDE$ və $AGFC$ isə bu üçbucağın $AB$ və $AC$ tərəflərində qurulmuş iki ixtiyarı paraleloqramlardır. Bu paraleloqramların $DE$ və $FG$ tərəflərini kəsişənə qədər uzadaq. Kəsişmə nöqtələrini $H$ ilə işarə edək. Onda $AH$ parçasinı yaradam kimi götürüb üçbucağın $BC$ tərəfində $BCML$ paraleloqramını quraq. Əgər $BL$ və $CM$ parçaları $AH$ parçasina paralel və bərabərdirsə onda sahələr üçün aşağıdakı bərabərlik doğrudur.

$$S_{ABDE}+S_{AGFC} = S_{BCML}$$

Şəkil 1

İsbatı: $BCML$ dördbucaqlısını şəkildəki kimi quraq. Qurmaya görə

$$AH=BL=CM$$

$AH$ ilə $MC$ və $AC$ ilə $FG$ düz xətləri bir-birinə paralel olduğundan onların kəsişməsində $AHVC$ paraleloqramı alınır. Deməli, $AH=CV$, çünki onlar $AHVC$ paraleloqramının qarşı tərəfləridir. Digər tərəfdən isə $AG=CF$, çünki onlar da $AGFC$ paraleloqramının qarşı tərəfləridir. Bu iki paraleloqramdan daha iki bərabərlik alınır. $HV=AC$ və $GF=AC$ . Deməli,

$$HV=GF \Rightarrow HG+CV=CV+VF \Rightarrow HG=VF$$

Biz aldıq ki, $\triangle AGH$ və $\triangle CFV$-də üç tərəf bərabərdir. Deməli bu üçbucaqlar bərabərdir. Eynilə $ABDE$ və $ABUH$ paraleloqramlarından alırıq ki, $\triangle AHE=\triangle BUD$.

Deməli, $S_{\triangle AGH} =S_{\triangle CFV}$ və $S_{\triangle AHE}=S_{\triangle BUD}$. Aldığımız iki cüt bərabər üçbucaqların yerlərini dəyişsək, yəni $\triangle CFV$-ni kəsib $\triangle AGH$-ın yerinə, $\triangle BUD$-ni isə $\triangle AHE$-nin yerinə qoysaq sahələr dəyişməz.

Şəkil 2

İndi isə bu yerdəyişmədən sonra alınan fiqura baxaq. Yenə $AHVC$ paraleloqramından alırıq ki, $AC=HV$. $ABUH$ paraleloqramından isə alırıq ki, $AB=HU$. $BCVU$ dördbucaqlısının isə $VC$ və $UB$ qarşı tərəfləri qurmaya görə paralel və bərabərdir. Deməli $BCVU$ paraleloqramdır. Buradan da alırıq ki, $BC=UV$. Nəticədə biz aldıq ki, $\triangle ABC = \triangle HUV$. Deməli $S_{\triangle HUV}=S_{\triangle ABC}$, yəni $\triangle HUV$-ni də kəsib $\triangle ABC$-nin yerinə qoysaq $BCML$ paraleloqramına bərabər olan $UVCB$ paraleloqramı almış oluruq ki, bunların da sahələri bərabərdir. $UVCB$ paraleloqramını biz $ABDE$ və $AGFC$ paraleloqramlarından (bax Şəkil 1) düzəltdiyimiz üçün onun sahəsi bu iki paraleloqramın sahələri cəminə bərabərdir.

Digər məqalələr

Apolloniy teoremi

Üçbucağın oturacağına median çəkilibsə, onun yan tərəflərinin kvadratları cəmi, medianın kvadratı ilə oturacağının yarısının kvadratı cəminin iki mislinə bərabərdir.

Çeva teoremi

İtalyan riyaziyyatçısı və mühəndisi Covanni Çeva XVII-XVIII əsrlərdə yaşamışdır. Çeva teoremi üçbucağın təpələrindən çəkilmiş şüaların bir nöqtədə kəsişməsi üçün zəruri və kafi şərt verir.

Qauss teoremi

Tutaq ki, düz xətt üçbucağın iki tərəfini və üçüncü tərəfin uzantısını kəsir. Onda, kəsişmə nöqtələrini qarşı təpələrlə birləşdirən parçaların orta nöqtələri bir düz xətt üzərindədir.

Napoleon teoremi

Əgər ixtiyari üçbucağın tərəflərində bərabərtərəfli üçbucaqlar qursaq, onların mərkəzləri də bərabərtərəfli üçbucağın təpəsi olacaq. İlk dəfə bu teoremi Vilyam Rezerford Napoleonun ölümündən 4 il sonra çap elətdirib.

Üçbucaq üçün Van-Obel teoremi

ABC üçbucağının daxilində O nöqtəsində kəsişən üç AA1, BB1 və CC1 çevianları üçün belə bir bərabərlik doğrudur: CO/OC1 = CA1/A1B + CB1/B1A

Menelay teoremi

Tutaq ki, düz xətt ABC üçbucağını kəsir. Bu xətt AB tərəfini C1, BC tərəfini A1, AC tərəfinin uzantısını isə B1 nöqtəsində kəsirsə, AC1/C1B, BA1/A1C və CB1/B1A nisbətlərinin hasili vahidə bərabərdir. Bu şərt həm də A1, B1 və C1 nöqtələrinin bir düz xətt üzərində olması üçün kafidir.

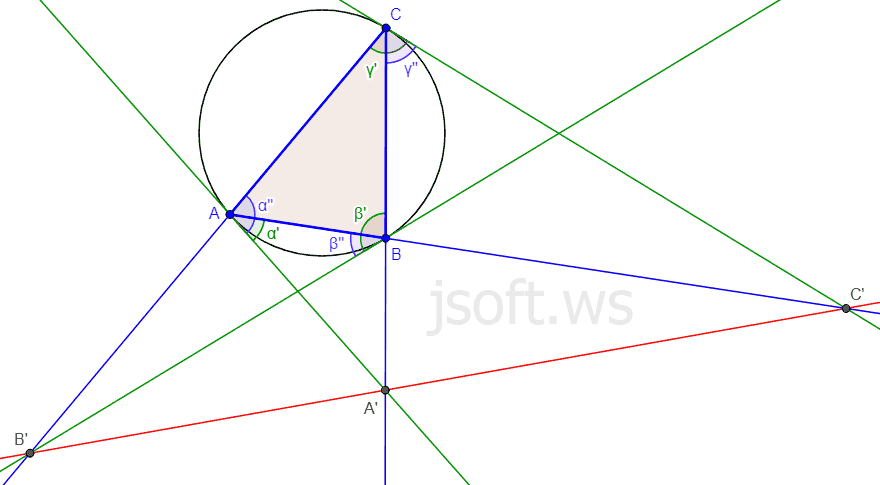
Üçbucaq üçün Paskal teoremi

Tutaq ki, bərabəryanlı olmayan ABC üçbucağının xaricinə çevrə çəkilib. Bu çevrəyə A, B və C nöqtələrində toxunanlar çəkilib. A’, B’ və C’ nöqtələri isə həmin toxunanların ABC üçbucağının tərəflərinin uzantıları ilə kəsişmə nöqtələridir. Onda A’, B’ və C’ nöqtələri bir düz xətt üzərindədir.

Jerqon nöqtəsi və Jerqon teoremi

Üçbucağın daxilinə çəkilmiş çevrənin tərəflərlə toxunma nöqtələrini qarşı təpələrlə birləşdirən parçaların kəsişmə nöqtəsi Jerqon nöqtəsi adlanır.