Ana səhifə :: Riyaziyyat :: Həndəsə :: Üçbucaq
Yaranma tarixi:
Oxşar üçbucaqlar
oxşar üçbucaq oxşarlıq əlamətlər
$\triangle ABC$ və $\triangle A_1B_1C_1$ o vaxt oxşar adlanır ki, $\angle A=\angle A_1$, $\angle B = \angle B_1$, $\angle C=\angle C_1$ və $\dfrac{AB}{A_1B_1}=\dfrac{BC}{B_1C_1}=\dfrac{AC}{A_1C_1}$.
Oxşar üçbucaqlar belə işarə olunur: $\triangle ABC \sim \triangle A_1B_1C_1$.
Lemma 1 Üçbucağın hər hansı tərəfinə paralel olub digər tərəfləri kəsən xətt, ondan oxşar üçbucaq ayırır.

İsbatı: Şəklə diqqət yetirsək görərik ki, $\triangle ABC$ və $\triangle MBN$-də $\angle B$ ortaqdır. $\angle BAC=\angle BMN$ və $\angle BCA = \angle BNM$, çünki bunlar uyğun bucaqlardır. Deməli hər üç bucaq bərabərdir.
İndi tərəflərin mütənasibliyinə baxaq. Ümumiləşmiş Fales teoreminə görə $\dfrac {AB}{BM} = \dfrac {BC}{BN}$.
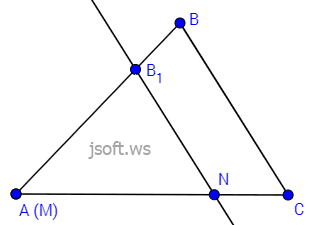
İndi $\triangle BMN$-i sürüşdürüb $M$ təpəsiini $A$ təpəsi üzərinə elə salaq ki, $MN$ tərəfi $AC$ tərəfi, $BM$ tərəfini isə $AB$ tərəfini özündə saxlayan xətt üzərində olsun. $\triangle BMN$-in $B$ təpəsini $AB$ xətti üzərində $B_1$ ilə işarə edək. Artıq bilirik ki, $\angle B_1NM = \angle BCA$. Xətlərin paralelliyinin ikinci əlamətinə görə $B_1N \parallel BC$. Onda yenə Fales teoreminə görə $\dfrac{AC}{MN}=\dfrac{AB}{B_1M}$. Bu şəkildəki $B_1M$ parçası isə yuxarıdakı şəkildəki $BM$ parçasıdır. Onda
$$\dfrac{AC}{MN} = \dfrac {AB}{BM} =\dfrac{BC}{BN}$$
Lemma 2: Əgər bir üçbucağın bucağı digər üçbucağın bucağına bərabərdirsə bu üçbucaqların sahələrinin nisbəti həmin bucağı əmələ gətirən tərəflərin hasilləri nisbətinə bərabərdir.

İsbatı: Tutaq ki, $\triangle ABC$ və $\triangle A_1B_1C_1$-də $\angle A=\angle A_1$. İsbat etməliyik ki,
$$\dfrac {S_{ABC}}{S_{A_1B_1C_1}} = \dfrac {AB\cdot AC}{A_1B_1 \cdot A_1C_1}$$

$A_1B_1C_1$ üçbucağını $ABC$ üçbucağı üzərinə elə yerləşdirək ki, $A_1$ təpəsi $A$ üzərinə düşsün, $A_1B_1$ və $A_1C_1$ tərəfləri isə uyğun olaraq $AB$ və $AC$ şüaları üzərində olsun. $\triangle ABC$ və $\triangle A_1B_1C$ eyni $CH$ hündürlüyünə malikdir. Ona görə
$\dfrac{S_{ABC}}{S_{A_1B_1C}} = \dfrac{\dfrac{AB\cdot CH}{2}} {\dfrac{A_1B_1\cdot CH}{2}} = \dfrac{AB}{A_1B_1}$
$\triangle A_1B_1C$ və $\triangle A_1B_1C_1$ həmçinin eyni $B_1H_1$ hündürlüyünə malikdir.
$\dfrac{S_{A_1B_1C}}{S_{A_1B_1C_1}} = \dfrac{\dfrac{AC\cdot B_1H_1}{2}} {\dfrac{A_1C_1\cdot B_1H_1}{2}} = \dfrac{AC}{A_1C_1}$
Bu iki nisbəti bir-birinə vursaq
$\dfrac{S_{ABC}}{S_{A_1B_1C}} \cdot \dfrac{S_{A_1B_1C}}{S_{A_1B_1C_1}} = \dfrac {AB\cdot AC}{A_1B_1 \cdot A_1C_1} \Rightarrow \dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac {AB\cdot AC}{A_1B_1 \cdot A_1C_1}$
Üçbucaqların oxşarlıq əlamətləri
Teorem (Üçbucaqların oxşarlığının birinci əlaməti): Əgər bir üçbucağın iki bucağı o biri üçbucağın iki bucağına bərabərdirsə bu üçbucaqlar oxşardır.
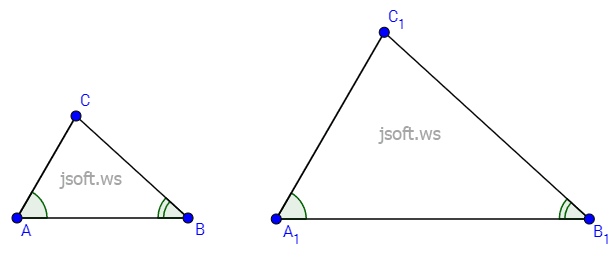
İsbatı: Tutaq ki, $\triangle ABC$ və $\triangle A_1B_1C_1$-də $\angle A =\angle A_1$, $\angle B=\angle B_1$. Onda üçbucağın daxili bucaqlarının cəmi $180°$ olduğu üçün
$\angle C=180°-\angle A -\angle B = 180° - \angle A_1 - \angle B_1 = \angle C_1$
Deməli bu üçbucaqların bütün bucaqları bərabərdir. İsbat etməliyik ki, bu üçbucaqların tərəfləri də mütənasibdir. Lemma 2-yə görə $\angle A=\angle A_1$ olduğu üçün
$\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac {AB \cdot AC} {A_1B_1 \cdot A_1C_1}$
$\angle B=\angle B_1$ olduğu üçün
$\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac {AB \cdot BC} {A_1B_1 \cdot B_1C_1}$
$\angle C=\angle C_1$ olduğu üçün
$\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac {AC \cdot BC} {A_1C_1 \cdot B_1C_1}$
Bu bərabərliklərin hamısında sol tərəf eyni olduğu üçün sağ tərəflər də eynidir.
$\dfrac {AB\cdot AC}{A_1B_1\cdot A_1C_1} = \dfrac {AB\cdot BC}{A_1B_1\cdot B_1C_1} \Rightarrow \dfrac{AC}{A_1C_1} = \dfrac {BC}{B_1C_1}$
$\dfrac {AB\cdot AC}{A_1B_1\cdot A_1C_1} = \dfrac {AC\cdot BC}{A_1C_1\cdot B_1C_1} \Rightarrow \dfrac{AB}{A_1B_1} = \dfrac {BC}{B_1C_1}$
Deməli,
$\dfrac {AC}{A_1C_1} = \dfrac {BC}{B_1C_1} = \dfrac {AB}{A_1B_1}$
Teorem isbat olundu.
Teorem (Üçbucaqların oxşarlığının ikinci əlaməti): Əgər bir üçbucağın iki tərəfi uyğun olaraq o biri üçbucağın iki tərəfi ilə mütənasib olub, bu tərəflərin əmələ gətirdiyi bucaqlar bərabərdirsə, bu üçbucaqlar oxşardır.

İsbatı: Tutaq ki, $\triangle ABC$ və $\triangle A_1B_1C_1$-də $\dfrac{AB}{A_1B_1}=\dfrac{AC}{A_1C_1}$ və $\angle A=\angle A_1$.
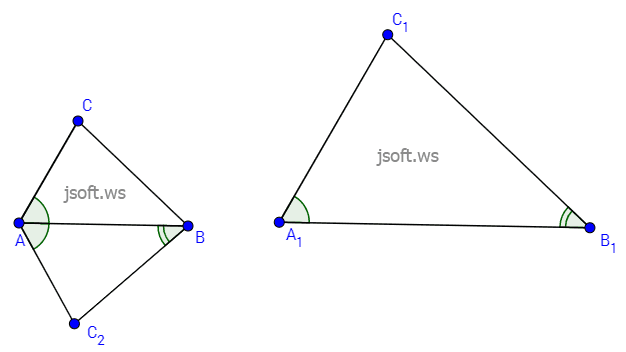
$ABC$ üçbucağına $AB$ tərəfi ortaq olan $ABC_2$ üçbucağını şəkildəki kimi əlavə edək. Yəni $C_2$ təpəsi $AB$ xəttinə nəzərən $C$ ilə müxtəlif yarımmüstəvilərdə yerləşsin, və $\angle C_2AB=\angle C_1A_1B_1$, $\angle C_2BA=\angle C_1B_1A_1 $. Üçbucaqların oxşarlığının birinci əlamətinə görə $\triangle ABC_2 \sim \triangle A_1B_1C_1$. Ona görə $\dfrac {AB}{A_1B_1}=\dfrac {AC_2}{A_1C_1}$. Şərtə görə isə $\dfrac {AB}{A_1B_1}=\dfrac {AC}{A_1C_1}$. Bu iki bərabərlikdən alırıq ki, $AC_2 = AC$. Onda üçbucaqların bərabərliyinin birinci əlamətinə görə $\triangle ABC_2=\triangle ABC$.
$\triangle ABC_2$ isə $\triangle A_1B_1C_1$ ilə oxşar idi. Deməli, $\triangle ABC \sim \triangle A_1B_1C_1$. Teorem isbat olundu.
Teorem (Üçbucaqların oxşarlığının üçüncü əlaməti): Əgər bir üçbucağın üç tərəfi digər üçbucağın üç tərəfi ilə mütənasibdirsə, bu üçbucaqlar oxşardir.
İsbatı: Tutaq ki, $\triangle ABC$ və $\triangle A_1B_1C_1$-də
$\dfrac{AB}{A_1B_1}=\dfrac{BC}{B_1C_1}=\dfrac{AC}{A_1C_1}$
Yenə də $\triangle ABC$-yə $AB$ tərəfi ortaq olan $\triangle ABC_2$ əlavə edək ki, $\angle C_2AB=\angle C_1A_1B_1$, $\angle C_2BA = \angle C_1B_1A_1$. Üçbucaqların oxşarlığının birinci əlamətinə görə $\triangle ABC_2 \sim \triangle A_1B_1C_1$. Yəni
$\dfrac{AB}{A_1B_1}=\dfrac{AC_2}{A_1C_1}=\dfrac{BC_2}{B_1C_1}$
Bu bərabərlikləri teoremin şərtindəki bərabərliklərlə müqayisə etsək aşağıdakıları alarıq.
$\dfrac {BC}{B_1C_1}=\dfrac{BC_2}{B_1C_1} \Rightarrow BC = BC_2$
$\dfrac {AC}{A_1C_1}=\dfrac{AC_2}{A_1C_1} \Rightarrow AC=AC_2$
Onda üçbucaqların bərabərliyinin üçüncü əlamətinə görə $\triangle ABC = \triangle ABC_2$. Yəni $ABC$ üçbucağı $A_1B_1C_1$ ilə oxşar olan $ABC_2$ üçbucağına bərabərdir. Deməli, $\triangle ABC \sim \triangle A_1B_1C_1$. Teorem isbat olundu.
Məsələ
Əvvəlcə özünüz həll etməyə çalışın
Məsələ 1: Tutaq ki, üçbucağın 3 hündürlüyü çəkilib. Üçbucağın hər bir tərəfinin uzunluğunun qarşı təpədən hündürlüklərin kəsişmə nöqtəsinə qədər məsafəsinə nisbətləri hasılınin bu nisbətlərin cəminə bərabər olduğunu isbat edin.
$\dfrac{AB}{CO} + \dfrac{BC}{AO} + \dfrac{CA}{BO} = \dfrac{AB}{CO} \cdot \dfrac{BC}{AO} \cdot \dfrac{CA}{BO}$

Digər məqalələr

Üçbucaqların həlli
Üçbucağın həlli dedikdə verilmiş 3 element vasitəsilə onun bütün tərəflərinin və bucaqlarının tapılması nəzərdə tutulur. Bu məsələni üç halda araşdıracağıq.

Üçbucaq
Üç təpəsi və üç tərəfi olan qapalı həndəsi fiqura üçbucaq deyilir. Üçbucağın təpəsini qarşı tərəfin ortası ilə birləşdirən düz xətt parçasına median deyilir. Üçbucağın təpəsindən qarşı tərəfə endirilən perpendikulyara onun hündürlüyü deyilir. Üçbucağın təpə bucağını yarı bölən xəttə tənbölən deyilir.
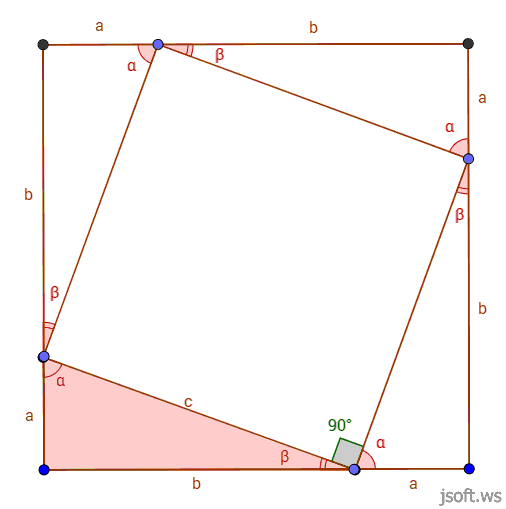
Pifaqor teoremi
Düzbucaqlı üçbucağın katetlərinin kvadratları cəmi hipotenuzun kvadratına bərabərdir. Bu teoremin 370 müxtəlif isbatı mövcuddur. Burada onlardan 5-i verilib.

Üçbucaqların bərabərlik əlamətləri
İki tərəf və arasındakı buçağı bərabər olan üçbucaqlar bərabərdir. Bir tərəf və ona söykənən bucaqları bərabər olan üçbucaqlar bərabərdir.

Bərabərtərəfli üçbucaq
Bütün tərəfləri bərabər olan üçbucağa bərabərtərəfli üçbucaq deyilir. Bərabərtərəfli üçbucaqda bütün bucaqlar 60°-dir. Belə üçbucaqlarda median, hündürlüyk və tənbölənlər üst-üstə düşür.

Kosinuslar teoremi
Üçbucağın istənilən tərəfinin kvadratı, qalan iki tərəfin kvadratları cəmi ilə onların hasilinin iki mislinin aralarındakı bucağın kosinusuna hasilinin fərqinə bərabərdir.

Sinuslar teoremi
Üçbucağın tərəfləri qarşı bucaqların sinusları ilə mütənasibdir. Bunu isbat etmək üçün isbat etməliyik ki, üçbucağın sahəsi onun ixtiyarı iki tərəfinin uzunluqları hasilinin yarısı ilə bu tərəflər arasında qalan bucağın sinusu hasilinə bərabərdir.
Üçbucaq bərabərsizliyi
Üçbucağın istənilən tərəfi digər iki tərəfin cəmindən kiçikdir. Üçbucağın böyük tərəfi qarşısında böyük bucağı durur. Üçbucağın böyük bucağı qarşısında böyük tərəfi durur.

Median, tənbölən, hündürlük
Üçbucağın medianları bir nöqtədə kəsişib bu kəsişmə nöqtəsində təpədən 2:1 nisbətində bölünür. Üçbucağın tənbölənləri bir nöqtədə kəsişib qarşı tərəfi bitişik tərəflərlə mütənasib hissələrə bölür. Üçbucağın hündürlükləri bir nöqtədə kəsişir.

Fales teoremi
Əgər bucağın tərəflərini kəsən xətlər onun bir tərəfində bərabər parçalar ayırırsa, o biri tərəfində də bərabər parçalar ayırır. Bucağın tərəflərini kəsən paralel xətlər onları mütənasib hissələrə bölür.

Heron düsturu
Bizim Eranın I əsrində yaşamış İskəndəriyyəli Heron həndəsə, mexanika, hidrostatika və optika ilə məşğul olurdu. Onun verdiyi Heron düsturunun köməyi ilə sahəni üç tərəf vasitəsilə tapmaq mümkündür.

Üçbucağın bucaqlarının cəmi
Üçbucağın daxili bucaqlarının cəmi 180°-yə bərabərdir. Üçbucağın xarici bucağı onunla qonşu olmayan iki daxili bucağın cəminə bərabərdir.
Oxşar üçbucaqların xassələri
Oxşar üçbucaqların perimetrlərinin nisbəti onların oxşarlıq əmsalına bərabərdir. Oxşar üçbucaqlarının xətti elementlərinin nisbəti üçbucaqların oxşarlıq əmsalına bərabərdir.
© Müəllif hüquqları qorunur
Bu saytdakı bütün məqalələr Cəfər N.Əliyev tərəfindən yazılıb. Onlar hər hansı üçüncu şəxs tərəfindən digər resurslarda çap edilərsə mənbə və müəllifin adı göstərilməlidir. Sayt özü həmin şərtlərə əməl edir.
