Дата создания:
Понятие многофокусных эллипсов (часть II)
эллипс
Теоремы. Замечания. Определения
Теорема 1
Каждая линия $L_k, k=1-6$ является частью обычного эллипса. Точно также как в $(7)$ упрощая уравнение $(2)$ линии $L_2$ и определяя их производные, получаем, что эти производные для линий $L_1$ и $L_2$ , когда точка $M$ стремится к точке $M_{23}$ , совпадают справа и слева, т.е. линия $L$ является гладкой (производная является непрерывной). Но второй порядок производной в точках $M_{ij}$ терпит разрыв первого рода (т.е. вторые производные линии $L$ в точках $M_{ij}$ являются разрывными).
Доказательство
Покажем, что линия $L$ в точке $P_{23}$ имеет неприрывные производные
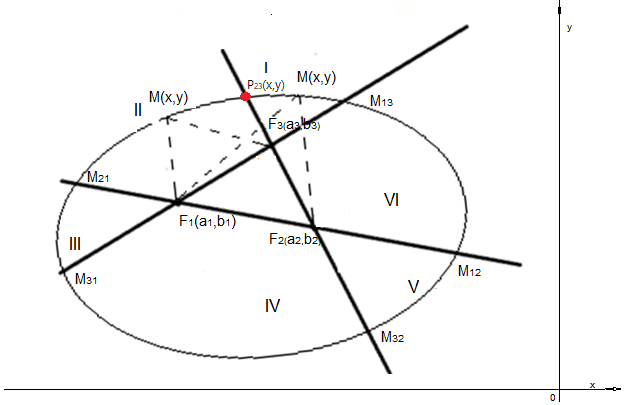
Рисунок 3
Возьмем любой $M$ из $I$ области:
\[ \begin{aligned} |F_1 M|+|F_2 M|=2a-|F_1 F_2| \end{aligned} \] \[ \begin{aligned} &\sqrt{(x-a_1)^2+(y-b_1)^2} + \sqrt{(x-a_2)^2+(y-b_2)^2}=2a-|F_1 F_2| \\[5pt] &\left(\dfrac{x-a_1}{|F_1 M|}+\dfrac{x-a_2}{|F_2 M|}\right)+\left(\dfrac{y-b_1}{|F_1 M|}+\dfrac{y-b_2}{|F_2 M|}\right)\cdot y'(x)=0\\[5pt] &\dfrac{x-a_1}{|F_1 M|}= \cos(x, F_1 M); \quad\dfrac{x-a_2}{|F_2 M|}= \cos(x, F_2 M) \\[5pt] &\dfrac{y-b_1}{|F_1 M|}= \cos(y, F_1 M); \quad\dfrac{y-b_2}{|F_2 M|}= \cos(y, F_2 M) \\ \end{aligned} \]
Используя все вышеперечисленные замены, получим:
\[ \begin{aligned} &y'(x) = - \dfrac{\cos(x, F_1 M) + \cos(x, F_2 M)}{\cos(y, F_1 M) + \cos(y, F_2 M)} \end{aligned} \]
Теперь, возьмем любой $M$ из $II$ области:
\[ \begin{aligned} |F_1 M|+|F_3 M|=2a-|F_1 F_2|-|F_2 F_3| \end{aligned} \] \[ \begin{aligned} &\sqrt{(x-a_1)^2+(y-b_1)^2} + \sqrt{(x-a_3)^2+(y-b_3)^2}=2a-|F_1 F_2|-|F_2 F_3| \\[5pt] &\left(\frac{x-a_1}{|F_1 M|}+\frac{x-a_3}{|F_3 M|}\right)+\left(\frac{y-b_1}{|F_1 M|}+\frac{y-b_3}{|F_3 M|}\right)\cdot y'(x)=0\\[5pt] &\frac{x-a_1}{|F_1 M|}= \cos(x, F_1 M); \quad\frac{x-a_3}{|F_3 M|}= \cos(x, F_3 M) \\[5pt] &\frac{y-b_1}{|F_1 M|}= \cos(y, F_1 M); \quad\frac{y-b_3}{|F_3 M|}= \cos(y, F_3 M) \\ \end{aligned} \]
Используя все вышеперечисленные замены, получим:
\[ \begin{aligned} &y'(x) = - \frac{\cos(x, F_1 M) + \cos(x, F_3 M)}{\cos(y, F_1 M) + \cos(y, F_3 M)} \end{aligned} \]
Затем устремляем $M$ к $P_{23}$ для обоих $y'(x)$:
\[ \begin{aligned} &y'(x) = - \frac{\cos(x, F_1 P_{23}) + \cos(x, F_2 P_{23})}{\cos(y, F_1 P_{23}) + \cos(y, F_2 P_{23})}\\[5pt] &y'(x) = - \frac{\cos(x, F_1 P_{23}) + \cos(x, F_3 P_{23})}{\cos(y, F_1 P_{23}) + \cos(y, F_3 P_{23})} \end{aligned} \]
Как видно из Рис.3 $\cos(x,F_2P_{23})$ равен $\cos(x,F_3P_{23})$, также как и $\cos(y,F_2P_{23})$ равен $\cos(y,F_3P_{23})$ что и требовалось доказать.
Теперь докажем, что второй порядок производной линии $L$ в точке $P_{23}$ терпит разрыв первого рода.
Возьмем любой $M$ из $I$ области:
\[ \begin{aligned} &\left(\dfrac{F_1 M-(x-a_1)\dfrac{x-a_1}{F_1 M}}{F_1 M^2}+\dfrac{F_2 M-(x-a_2)\dfrac{x-a_2}{F_2 M}}{F_2 M^2}\right)+\left(-\dfrac{(y-b_1)\dfrac{x-a_1}{F_1 M}}{F_1 M^2}-\dfrac{(y-b_2)\dfrac{x-a_2}{F_2 M}}{F_2 M^2}\right)\cdot y'(x)+ \\[5pt] +&\left(\dfrac{y-b_1}{F_1 M}+\dfrac{y-b_2}{F_2 M}\right)\cdot y''(x)+\left(-\dfrac{(x-a_1)\dfrac{y-b_1}{F_1 M}}{F_1 M^2}-\dfrac{(x-a_2)\dfrac{y-b_2}{F_2 M}}{F_2 M^2}\right)\cdot y'(x)+ \\[5pt] +&\left(\dfrac{F_1 M-(y-b_1)\dfrac{y-b_1}{F_1 M}}{F_1 M^2}+\dfrac{F_2 M-(y-b_2)\dfrac{y-b_2}{F_2 M}}{F_2 M^2}\right)\cdot y'^2(x)=0\\[5pt] &(\cos(y,F_1 M) + \cos(y,F_2 M))\cdot y''(x)= - \dfrac{F_1M^2-(x-a_1)^2}{F_1M^3} - \dfrac{F_2M^2-(x-a_2)^2}{F_2M^3} +\\[5pt] +&2\left(\dfrac{(x-a_1)(y-b_1)}{F_1M^3}+\dfrac{(x-a_2)(y-b_2)}{F_2M^3} \right)\cdot y'(x)-\\[5pt] -&\left(\dfrac{F_1 M^2-(y-b_1)^2)}{F_1M^3}+\dfrac{F_2 M^2-(y-b_2)^2)}{F_2M^3} \right)\cdot y'^2(x)= -\dfrac{(y-b_1)^2}{F_1M^3}-\dfrac{(y-b_2)^2}{F_2M^3}+\\[5pt] +&2\left(\dfrac{\cos(x,F_1 M)\cos(y,F_1 M)}{F_1M}+\dfrac{\cos(x,F_2 M)\cos(y,F_2 M)}{F_2M} \right)\cdot y'(x)-\\[5pt] -&\left(\dfrac{(x-a_1)^2}{F_1M^3}+\dfrac{(x-a_2)^2}{F_2M^3} \right)\cdot y'^2(x) \end{aligned} \]
Далее получаем выражение для второй производной из области $I$:
\[ \begin{aligned} &(\cos(y, F_1 M) + \cos(y, F_2 M))\cdot y''(x) = -\dfrac{\cos^2(x, F_1 M)}{F_1 M} -\dfrac{\cos^2(y, F_2 M)}{F_2 M}+\\[5pt] +&2\left(\dfrac{\cos(x, F_1 M) \cdot \cos(y, F_1 M)}{F_1 M}+\dfrac{\cos(x, F_2 M) \cdot \cos(y, F_2 M)}{F_2 M}\right)\cdot y'(x)-\\[5pt] -&\left(\dfrac{\cos^2(x, F_1 M)}{F_1 M} + \dfrac{\cos^2(x, F_2 M)}{F_2 M}\right)\cdot y'(x) \end{aligned} \]
Теперь, возьмем любой $M$ из $II$ области:
\[ \begin{aligned} &\left(\dfrac{F_1 M-(x-a_1)\dfrac{x-a_1}{F_1 M}}{F_1 M^2}+\dfrac{F_3 M-(x-a_3)\dfrac{x-a_3}{F_3 M}}{F_3 M^2}\right)+\left(-\dfrac{(y-b_1)\dfrac{x-a_1}{F_1 M}}{F_1 M^2}-\dfrac{(y-b_3)\dfrac{x-a_3}{F_3 M}}{F_3 M^2}\right)\cdot y'(x)+ \\[5pt] +&\left(\dfrac{y-b_1}{F_1 M}+\dfrac{y-b_3}{F_3 M}\right)\cdot y''(x)+\left(-\dfrac{(x-a_1)\dfrac{y-b_1}{F_1 M}}{F_1 M^2}-\dfrac{(x-a_3)\dfrac{y-b_3}{F_3 M}}{F_3 M^2}\right)\cdot y'(x)+ \\[5pt] +&\left(\dfrac{F_1 M-(y-b_1)\dfrac{y-b_1}{F_1 M}}{F_1 M^2}+\dfrac{F_3 M-(y-b_3)\dfrac{y-b_3}{F_3 M}}{F_3 M^2}\right)\cdot y'^2(x)=0\\[5pt] &(\cos(y,F_1 M) + \cos(y,F_3 M))\cdot y''(x)= - \dfrac{F_1M^2-(x-a_1)^2}{F_1M^3} - \dfrac{F_3M^2-(x-a_3)^2}{F_3M^3} +\\[5pt] +&2\left(\dfrac{(x-a_1)(y-b_1)}{F_1M^3}+\dfrac{(x-a_3)(y-b_3)}{F_3M^3} \right)\cdot y'(x)-\\[5pt] -& \left(\dfrac{F_1 M^2-(y-b_1)^2)}{F_1M^3}+\dfrac{F_3 M^2-(y-b_3)^2)}{F_3M^3} \right)\cdot y'^2(x)= -\dfrac{(y-b_1)^2}{F_1M^3}-\dfrac{(y-b_3)^2}{F_3M^3}+\\[5pt] +&2\left(\dfrac{\cos(x,F_1 M)\cos(y,F_1 M)}{F_1M}+\dfrac{\cos(x,F_3 M)\cos(y,F_3 M)}{F_3M} \right)\cdot y'(x)-\\[5pt] -&\left(\dfrac{(x-a_1)^2}{F_1M^3}+\dfrac{(x-a_3)^2}{F_3M^3} \right)\cdot y'^2(x) \end{aligned} \]
Далее получаем выражение для второй производной из области $II$:
\[ \begin{aligned} &(\cos(y, F_1 M) + \cos(y, F_3 M))\cdot y''(x) = -\dfrac{\cos^2(x, F_1 M)}{F_1 M} -\dfrac{\cos^2(y, F_3 M)}{F_3 M}+\\[5pt] +&2\left(\dfrac{\cos(x, F_1 M) \cdot \cos(y, F_1 M)}{F_1 M}+\dfrac{\cos(x, F_3 M) \cdot \cos(y, F_2 M)}{F_3 M}\right)\cdot y'(x)-\\[5pt] -&\left(\dfrac{\cos^2(x, F_1 M)}{F_1 M} + \dfrac{\cos^2(x, F_3 M)}{F_3 M}\right)\cdot y'(x) \end{aligned} \]
Затем устремляем $M$ к $P_{23}$ для обоих $y''(x)$:
Для $I$:
\[ \begin{aligned} &(\cos(y, F_1 P_{23}) + \cos(y, F_2 P_{23}))\cdot y''(x) = -\dfrac{\cos^2(x, F_1 P_{23})}{F_1 P_{23}} -\dfrac{\cos^2(y, F_2 P_{23})}{F_2 P_{23}}+\\[5pt] +&2\left(\dfrac{\cos(x, F_1 P_{23}) \cdot \cos(y, F_1 P_{23})}{F_1 P_{23}}+\dfrac{\cos(x, F_2 P_{23}) \cdot \cos(y, F_2 P_{23})}{F_2 P_{23}}\right)\cdot y'(x)-\\[5pt] -&\left(\dfrac{\cos^2(x, F_1 MP_{23})}{F_1 P_{23}} + \dfrac{\cos^2(x, F_2 P_{23})}{F_2 P_{23}}\right)\cdot y'(x)\\ \end{aligned} \]
Для $II$:
\[ \begin{aligned} &(\cos(y, F_1 P_{23}) + \cos(y, F_3 P_{23}))\cdot y''(x) = -\dfrac{\cos^2(x, F_1 P_{23})}{F_1 P_{23}} -\dfrac{\cos^2(y, F_3 P_{23})}{F_3 P_{23}}+\\[5pt] +&2\left(\dfrac{\cos(x, F_1 P_{23}) \cdot \cos(y, F_1 P_{23})}{F_1 P_{23}}+\dfrac{\cos(x, F_3 P_{23}) \cdot \cos(y, F_2 P_{23})}{F_3 P_{23}}\right)\cdot y'(x)-\\[5pt] -&\left(\dfrac{\cos^2(x, F_1 P_{23})}{F_1 P_{23}} + \dfrac{\cos^2(x, F_3 P_{23})}{F_3 P_{23}}\right)\cdot y'(x) \end{aligned} \]
вывод для вторых производных:
- так как $F_3$ и $F_2$ лежат на прямой $F_2P_{23}$ коэффиценты $y''(x)$ одинаковы.
- $y''(x)$ при $x=x_{23}$ терпит разрыв первого рода, т.е. получает скачок.
- если касательная к линии $L$ в точке $ P_{23} $ параллельна к оси $x$, то тогда $y'(x)=0$, и достаточно того, что $F_2P_{23} \neq F_3P_{23}$ !!!
Замечание 1
Три прямые $\overline{F_1F_2}$, $\overline{F_1F_3}$, $\overline{F_2F_3}$ разбивают плоскость на 6 неограниченных частей. Дуга, лежащая в $I$ полости $\breve{M_{13}M_{23}}$, является частью эллипса с фокусами $F_1$ и $F_2$. Большой полуосью этого эллипса является:
\[\dfrac{l-|F_1 F_2 |}{2}\]
а малая полуось:
\[\dfrac{\sqrt{l^2-2l|F_1 F_2 |}} {2}\]
где $l$- постоянное число (длина нити).
Симметрично этому в $IV$ полости находится дуга $\breve{M_{31} M_{32}}$, которая является частью эллипса с фокусами $F_1$ и $F_2$, как в предыдущем случае. Для него большой полуосью является:
\[\dfrac{l-|F_1 F_3 |-|F_2 F_3 |)}{2}\]
а малая полуось:
\[\dfrac{\sqrt{(l-|F_1 F_3 |-|F_2 F_3 |)^2-|F_1 F_2 |^2 }}{2}\]
Аналогично находим для $II$, $III$, $V$, $VI$ полостей. Для $II$ полости дуга $\breve{M_{21}M_{23}}$ является частью эллипса с фокусами $F_1$ и $F_3$. Большой полуосью этого эллипса является:
\[\dfrac{l-|F_1 F_2 |-|F_2 F_3 |}{2}\]
а малая полуось :
\[\dfrac{\sqrt{(l-|F_1 F_2 |-|F_2 F_3 |)^2-|F_1 F_3 |^2}}{2}\]
Симметрично этому в $V$ полости находится дуга $\breve{M_{12}M_{32}}$, которая является частью эллипса в тех же фокусах $F_1$ и $F_3$. Для этого эллипса большой полуосью является:
\[\dfrac{l-|F_1 F_3 |}{2}\]
а малая полуось
\[\dfrac{\sqrt{l^2-2l|F_1 F_3 |}}{2}\]
Наконец в $III$ полости дуга $\breve{M_{31}M_{21}}$ является частью эллипса с фокусами $F_2$ и $F_3$. Большой полуосью этого эллипса является:
\[\dfrac{l-|F_2 F_3 |}{2}\]
а малая полуось:
\[\dfrac{\sqrt{l^2-2l|F_2 F_3 |}}{2}\]
Симметрично этому в $VI$ полости находится дуга $\breve{M_{13}M_{12}}$, которая является частью эллипса в тех же фокусах $F_2$ и $F_3$, но большая полуось этого эллипса имеет вид:
\[\dfrac{l-|F_1 F_3 |-|F_2 F_1 |}{2}\]
а малая полуось:
\[\dfrac{\sqrt{(l-|F_1 F_3 |-|F_2 F_1 |)^2-|F_2 F_3 |^2}}{2}\]
Определение
Полученная линия $L$ образованная с помощью гладкого соединения шести различных эллипсов не является обычным эллипсом, а называется трехфокусным эллипсом.
Полный текст статьи в формате PDF
Автор статьи: Алиева Захра
Читайте также

Понятие многофокусных эллипсов (часть III)
Третья часть статьи про Многофокусные эллипсы. Уравнения-неравенства, образующиe один эллипс и задающие все шесть участков разных эллипсов, из которых состоит трехвокусный эллипс.

Понятие многофокусных эллипсов (часть I)
Излагаемая работа посвящена трехфокусному и многофокусному эллипсу. Здесь будет приведено, как построение этих эллипсов, так и аналитический вид уравнения этих эллипсов, что является первичной публикацией в этом направлении.
© Все права защищены
Все статьи этого сайта написаны Джафаром Н.Алиевым. Перепечатывание любой статьи на стороннем ресурсе должно сопровождаться именем автора и ссылкой на данный ресурс. Сам автор следует этим правилам.
