Ana səhifə :: Riyaziyyat :: Həndəsə :: Üçbucaq
Yaranma tarixi:
Dezarq teoremi
üçbucaq Menelay Fales
Jirar Dezarq (1591-1661) proyektiv həndəsənin özülünü qoyanlardandır. Bu fransız riyaziyyatçısı həm də memar və hərbi mühəndis olmuşdur.
Teorem: Əgər $\triangle ABC$ və $\triangle A_1B_1C_1$-in təpə nöqtələrini birləşdirərkən $AA_1$, $BB_1$ və $CC_1$ düz xətləri bir nöqtədə kəsişərsə və ya üçü də paralel olarsa, onsa $AB$ ilə $A_1B_1$, $BC$ ilə $B_1C_1$, $AC$ ilə $A_1C_1$ düz xətləri kəsişirsə, bu kəsişmə nöqtələri bir düz xətt üzərindədir.

Şəkil 1
İsbatı: Teoremdə belə bir şərt qoyulur ki, əgər tərəflərin uzantıları kəsişərsə bu kəsişmə nöqtələri bir düz xətt üzərində olacaq. Doğrudan da, əgər üçbucaqların tərəfləri paralel olarsa onların uzantıları kəsişməyəcək.
Teoremin isbatını iki hal üçün aparmalıyıq. Əvvəlcə tutaq ki, $AA_1$, $BB_1$ və $CC_1$ düz xətləri hər hansı $S$ nöqtəsində kəsişir. Tərəflərin uzantılarının kəsişmə nöqtələrini belə işarə edək.
$$AB \cap A_1B_1 = P\\
BC \cap B_1C_1 = Q\\
CA \cap C_1A_1 = R$$
$\triangle SAB$ və $A_1B_1$ xəttinə Menelay teoremini tətbiq etsək
$$\dfrac{SA_1}{A_1A} \cdot \dfrac{AP}{PB} \cdot \dfrac{BB_1}{B_1S} = 1$$
Eyni teoremi $\triangle SBC$-yə və $B_1C_1$ düz xəttinə tətbiq etsək
$$\dfrac{SB_1}{B_1B} \cdot \dfrac{BQ}{QC} \cdot \dfrac{CC_1}{C_1S} = 1$$
$\triangle SCA$ və $C_1A_1$ xəttinə də həmin teoremin tətbiq edib aşağıdakı bərabərliyi alarıq.
$$\dfrac{SC_1}{C_1C} \cdot \dfrac{CR}{RA} \cdot \dfrac{AA_1}{A_1S} = 1$$
Bu üç bərabərliyi tərəf-tərəfə vursaq belə bir bərabərlik alarıq.
$$\left(\frac{AP}{PB} \cdot \frac{BQ}{QC}\cdot \frac{CR}{RA}\right) \cdot \left( \frac{SA_1}{A_1A} \cdot \frac{AA_1}{A_1S} \right) \times \\
\times \left(\frac{SB_1}{B_1B} \cdot \frac{BB_1}{B_1S}\right) \cdot \left(\frac{SC_1}{C_1C} \cdot \frac{CC_1}{C_1S}\right)=1$$
Birinci mötərizədən başqa yerdə qalanların hamısı ixtisar olunur.
$$\frac{AP}{PB} \cdot \frac{BQ}{QC}\cdot \frac{CR}{RA}=1$$
Onda, Tərs Menelay teoreminə görə $P$, $Q$ və $R$ nöqtələri bir düz xətt üzərindədir.

Şəkil 2
İndi isə tutaq ki, $AA_1 || BB_1 || CC_1$. $AB$ ilə $A_1B_1$ və $BC$ ilə $B_1C_1$ tərəflərinin uzantılarının kəsişmə nöqtələrini və bu kəsişmə nöqtələrindən keçən düz xəttin üçüncü $AC$ və $A_1C_1$ tərəflərinin uzantıları ilə kəsişmə nöqtələrini aşağıdakı kimi işarə edək.
$$AB \cap A_1B_1 = P\\
BC \cap B_1C_1 = Q\\
PQ \cap AC = R\\
PQ \cap A_1C_1=R_1$$
Göstərməliyik ki, $R$ və $R_1$ nöqtələri üst-üstə düşür.
$\triangle BPQ$ və $AC$ düz xəttinə baxsaq Menelay teoreminə görə
$$\frac{BA}{AP} \cdot \frac{PR}{RQ} \cdot \frac{QC}{CB}=1$$
Eynilə $\triangle B_1PQ$ və $A_1C_1$ düz xətti üçün
$$\frac{B_1A_1}{A_1P} \cdot \frac{PR_1}{R_1Q} \cdot \frac{QC_1}{C_1B_1} = 1$$
Xətlərin paralelliyindən Fales teoreminə görə
$\dfrac{BA}{AP} = \dfrac {B_1A_1} {A_1P}$ və $\dfrac{QC}{CB}=\dfrac{QC_1}{C_1B_1}$
Onda bu iki nisbətin bərabərliyini nəzər alaraq yuxarıdakı iki münasibətdən aşağıdakı nəticəyə gəlirik.
$$\frac{PR}{RQ}=\frac{PR_1}{R_1Q}$$
Yəni $R$ və $R_1$ eyni nöqtələrdir. Bunanla da Dezarq teoremi bütünlüklə isbat olundu
Şəkil 1-ə baxsaq görərik ki, orada 10 nöqtə və 10 düz xətt var və hər bir düz xətt üzərində 3 nöqtə yerləşir. Hər bir nöqtədən isə 3 düz xətt keçir. Bu cür fiqura Dezarq konfiqurasiyası deyilir. $S$ nöqtəsinə dezarq nöqtəsi, $PQR$ xəttinə isə $ABC$ və $A_1B_1C_1$ üçbucaqları üçün dezarq xətti deyilir.
Digər məqalələr

Apolloniy teoremi
Üçbucağın oturacağına median çəkilibsə, onun yan tərəflərinin kvadratları cəmi, medianın kvadratı ilə oturacağının yarısının kvadratı cəminin iki mislinə bərabərdir.

Menelay teoremi
Tutaq ki, düz xətt ABC üçbucağını kəsir. Bu xətt AB tərəfini C1, BC tərəfini A1, AC tərəfinin uzantısını isə B1 nöqtəsində kəsirsə, AC1/C1B, BA1/A1C və CB1/B1A nisbətlərinin hasili vahidə bərabərdir. Bu şərt həm də A1, B1 və C1 nöqtələrinin bir düz xətt üzərində olması üçün kafidir.
Üçbucaq üçün Paskal teoremi
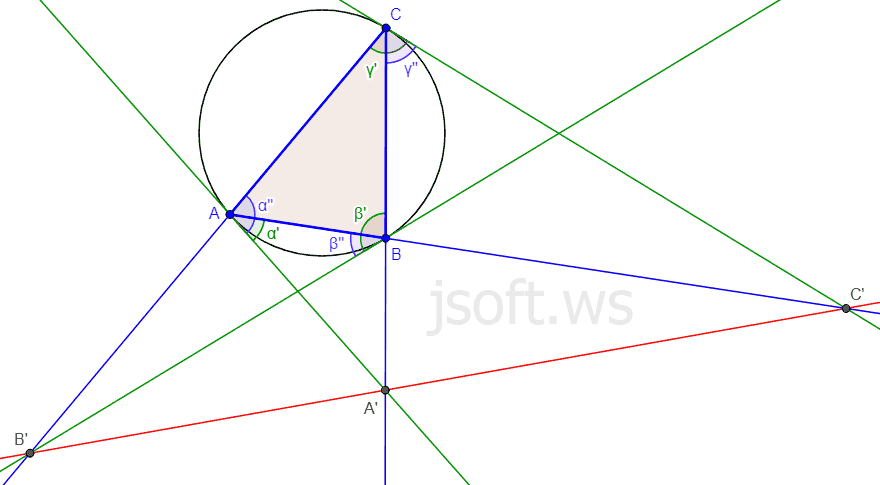
Tutaq ki, bərabəryanlı olmayan ABC üçbucağının xaricinə çevrə çəkilib. Bu çevrəyə A, B və C nöqtələrində toxunanlar çəkilib. A’, B’ və C’ nöqtələri isə həmin toxunanların ABC üçbucağının tərəflərinin uzantıları ilə kəsişmə nöqtələridir. Onda A’, B’ və C’ nöqtələri bir düz xətt üzərindədir.

Stüart teoremi
Üçbucağın oturacağı üzərində olan nöqtədən qarşı təpəyə qədər məsafənin kvadratının oturacağa hasili, digər iki tərəfin kvadratlarının oturacağın onlarla qonşu olmayan hissələrinə hasili cəmi ilə oturacaq və onun hissələrinin hasilinin fərqinə bərabərdir.

Morli teoremi
Bucağı üç bərabər hissəyə bölən şüaların hər birinə üçbölən deyilir. İstənilən üçbucağın qonşu üçbölənlərinin kəsişmə nöqtələri bərabərtərəfli üçbucağın təpə nöqtələridir.
© Müəllif hüquqları qorunur
Bu saytdakı bütün məqalələr Cəfər N.Əliyev tərəfindən yazılıb. Onlar hər hansı üçüncu şəxs tərəfindən digər resurslarda çap edilərsə mənbə və müəllifin adı göstərilməlidir. Sayt özü həmin şərtlərə əməl edir.
