Ana səhifə :: Riyaziyyat :: Həndəsə :: Dördbucaqlı
Yaranma tarixi:
Bərabəryanlı trapesiya
trapesiya xassə əlamətlər
Əgər trapesiyanın yan tərəfləri bərabərdirsə ona bərabəryanlı trapesiya deyilir.
Bərabəryanlı trapesiyanın xassələri
Xassə 1: Əgər trapesiyanın bir oturacağındakı bucaqlar bərabərdirsə, onun o biri oturacağındakı bucaqlar da bərabərdir.
İsbatı: Bunun isbatı çox trivialdır. Çünki trapesiyanın oturacaqları paralel olduğundan onun yan tərəfə bitişik bucaqlarının cəmi birtərəfli bucaqlar kimi $180°$ olacaq. Ona görə
$\angle A = \angle D \Rightarrow 180°-\angle B = 180°-\angle C \Rightarrow \angle B=\angle C$
Xassə 2: Bərabəryanlı trapesiyanın oturacağa bitişik bucaqları bərabərdir.

Şəkil 1
İsbatı: Trapesiyanın $B$ və $C$ təpələrindən hündürlüklərini çəksək iki bərabər düzbucaqlı üçbucaq alarıq. Bu üçbucaqlarda hipotenuz və bir katet bərabərdir. Ona görə $\angle A=\angle D$. Onda, əvvəlki xassəyə görə həm də $\angle B=\angle C$.
Xassə 3: Trapesiya bərabəryanlıdırsa onun diaqonalları da bərabərdir.

Şəkil 2
İsbatı: $\triangle ABD$ və $\triangle DCA$-da $AB=DC$, $AD$ tərəfi ortaq, $\angle A =\angle D$ olduğu üçün bu üçbucaqlar I əlamətə görə bərabərdir. Bərabərlikdən isə alınır ki.
$AC=BD$
Xassə 4: Bərabəryanlı trapesiyada diaqonallar oturacaqlar ilə eyni bucaq əmələ gətirir.

Şəkil 3
İsbatı: $\angle CAD=\angle ACB$ və $\angle ADB = \angle DBC$, çünki bunlar çarpaz bucaqlardır. $\triangle ABD$ və $\triangle DCA$ isə üç tərəfinə görə bərabərdir. Onda $\angle CAD = \angle ADB$. Bununla da bütün bucaqların bərabərliyi alındı.
$\angle CAD = \angle ADB = \angle DBC = \angle ACB$
Xassə 5: Bərabəryanlı trapesiyanın xaricinə çevrə çəkmək olar.
İsbatı: Bilirik ki, dördbucaqlının qarşı bucaqlarının cəmi $180°$ olarsa onun xaricinə çevrə çəkmək olar. Bərabəryanlı trapesiyada isə isbat etdiyimizə görə oturacağa bitişik bucaqlar bərabərdir.
$\angle BAD + \angle CBA = \angle BAD + \angle DCB = 180°$
Bərabəryanlı trapesiyanın əlamətləri
Əlamət 1: Əgər trapesiyanın oturacağa bitişik bucaqları bərabərdirsə bu trapesiya bərabəryanlıdır.
İsbatı: Şəkil 1-də $ABM$ və $DCN$ düzbucaqlı üçbucaqları katet və bitişik bucağa görə bərabərdir. Bərabərlikdən alırıq ki, $AB=CD$.
Əlamət 2: Əgər trapesiyanın diaqonalları bərabərdirsə bu trapesiya bərabəryanlıdır.
İsbatı: Şəkil 2-yə baxsaq $\triangle ABD$ və $\triangle DCA$-nın sahələri eynidir. Bu sahələrin sinuslar vasitəsilə ifadəsini yazaq.
$S_{\triangle ABD} = S_{\triangle DCA} \Rightarrow \dfrac{1}{2} AC \cdot AD \cdot sin \angle CAD = \dfrac{1}{2} DB \cdot AD \cdot sin \angle BDA \Rightarrow \\[15pt]
\Rightarrow sin \angle CAD = sin \angle BDA \Rightarrow \angle CAD = \angle BDA $
Onda $\triangle ABD$ və $\triangle DCA$ iki tərəfi və aralarındakı bucağa görə bərabərdir. Bu bərabərlikdən yan tərəflərin bərabərliyi alınır.
Əlamət 3: Əgər trapesiyanın diaqonalları oturacaqlar ilə bərabər bucaqlar əmələ gətirirsə bu trapesiya bərabəryanlıdır.
İsbatı: Şəkil 3-də $\triangle ABD$ və $\triangle DCA$-nın sahələri eynidir. Bu sahələrin sinuslar vasitəsilə ifadəsini yazaq.
$\dfrac{1}{2} AC \cdot AD \cdot sin \angle CAD = \dfrac{1}{2} DB \cdot AD \cdot sin \angle BDA \Rightarrow AC = DB$
Onda ikinci əlamətə görə trapesiya bərabəryanlıdır.
Əlamət 4: Əgər trapesiyanın xaricinə çevrə çəkmək olarsa bu trapesiya bərabəryanlıdır.
İsbatı: Əgər dördbucaqlının xaricinə çevrə çəkilibsə onun qarşı bucaqlarının cəmi 180°-yə bərabərdir. Yəni,
$\angle BCD + \angle BAD = 180°$
Həm də bilirik ki,
$\angle ABC + \angle BAD = 180°$
Deməli,
$\angle ABC = \angle BCD$
Eynilə alırıq ki,
$\angle BAD = \angle CDA$
Bu isə birinci əlamətə görə yan tərəflərin bərabərliyi deməkdir.
Məsələlər
Əvvəlcə özünüz həll etməyə çalışın
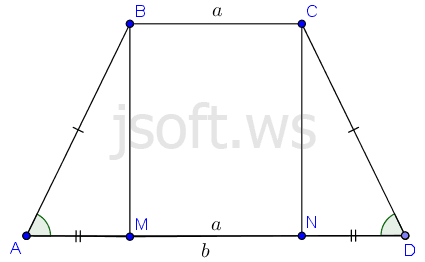
Məsələ 1: Bərabəryanlı $ABCD$ trapesiyasının $AD$ oturacağına $BM$ hündürlüyü çəkilib. $BC=a$, $AD=b$ olarsa, $AM$ və $MD$ parçalarının uzunluqlarını tapın.
Digər məqalələr

Trapesiya
Yalnız iki qarşı tərəfi paralel olan qabarıq dördbucaqlıya trapesiya deyilir. Bu paralel tərəflərə trapesiyanın oturacaqları, paralel olmayan tərəflərə isə yan tərəfləri deyilir. Trapesiyanın qarşı təpələrini birləşdirən düz xətt parçasına onun diaqonalı deyilir.

Trapesiyanın sahəsi
Trapesiyanın sahəsi oturacaqlarının cəmini yarısı ilə hündürlüyü hasilinə bərabərdir. Bu sahəni trapesiyanın diaqonalları ilə bu diaqonalların kəsişməsindən alınan bucağın sinusu hasilinin yarısı kimi də ifadə etmək olar.
© Müəllif hüquqları qorunur
Bu saytdakı bütün məqalələr Cəfər N.Əliyev tərəfindən yazılıb. Onlar hər hansı üçüncu şəxs tərəfindən digər resurslarda çap edilərsə mənbə və müəllifin adı göstərilməlidir. Sayt özü həmin şərtlərə əməl edir.
